Berechnungen zum E-Bike/Pedelec
|
Autor: |
Dieter Drewanz |
|
Begonnen: |
Oktober 2014 |
|
Stand: |
30.05.15 |
Table of Contents
1 Kräfte, die das Radfahren so mühsam werden lassen
1.1.1 Kräfte und Momente
1.1.2 Leistungen und Arbeit
3 Fahrtwiderstandsanteile durch Rollen und Wind
3.1 Rollwiderstand
3.2 Luftwiderstand
4 Bewegungsenergie oder kinetische Energie
5.2 Antriebsarten
5.3 Kennlinien von Antrieben und Dimensionierungseinflüsse
6.1 Beschleunigung ohne Fahrwiderstände (Verluste)
6.2 Beschleunigung mit Rollwiderstand
6.3 Beschleunigung mit Steigungswiderstand
6.4 Beschleunigung mit Luftwiderstand
6.5 Kombination aller Fahrwiderstände
7 Messung der eigenen Leistung und der Fahrwiderstände
7.1 Ermittlung der eigenen Pedalleistung
7.2 Ermittlung der Fahrwiderstände des Rades
8 Streckenmessung für eine Simulationsverwendung
8.1 Verwendung selbstaufgezeichneter GPS-Daten
8.2 Kombination mehrerer Streckenmessungen
8.3 Berücksichtigung der Antriebssystemeigenschaften
9 Der Nutzbremsbetrieb bzw. Rekuperation
9.1 Nutzbremsfahrt bei einer Bergfahrt mit Wirkungsgradbetrachtung
9.2 Technische Zusammenhänge bei der Rückspeisung
Ein Fahrrad/E-Bike/Pedelec durch die Muskelkraft angetrieben erforderte einen nicht unerheblichen Kraftaufwand. Wird statt der Muskelkraft oder zusätzlich zur Muskelkraft ein Motor für den Antrieb eingesetzt, muss dieser genügend Leistung und Kraft aufbringen um diese Fahrwiderstände zu überwinden. Diese lassen sich je nach Messgenauigkeit der jeweiligen physikalischen Größen und Zusammenhänge berechnen.
Wesentlich sind folgende Fahrwiderstandsursachen:
Steigungen
Beschleunigungen
Rollreibungen (Rad-Boden, Kette, Lager)
Luftreibungen
Zur Vereinfachung wird hierbei zunächst nicht zwischen Fahrrad, Pedelec, E-Bike unterschieden. Die Physik hinter den Effekten wird aufgezeigt und manchmal auch mehr oder weniger umgangssprachlich exakt verwendet. Einige hier angebrachten Beispiele dienen zur Verdeutlichung eines Effektes. Die Zusammenstellung soll keinen Literaturpreis gewinnen. Daher ist der Text sprachlich einfach gehalten und enthält auch einfache Reihungen und Exkurse, so dass der rote Faden nicht immer so klar ersichtlich ist.
An der steilsten Stelle einer Tiefgarage einer Wohnung zeigt das Smartphone mit Hilfe einer Anwendung zur Winkelmessung einen Steigungswinkel von etwa 10 bis 11 Grad an. Auf einer Länge von ungefähr 22m werden etwa 3m Höhe überwunden. Somit ergibt sich eine durchschnittliche Steigung von 13,6% bzw. Steigungswinkel von 7,8°. An der steilsten Stelle wäre es nach der Messung ein Steigungswinkel von 11° bzw. eine Steigung von 19,5%. Gut zu sehen hier ist die Schwierigkeit eine Steigung ohne professionelles Vermessungsgerät zu bestimmen, auf der anderen Seite soll sicherlich das Rad mit Motorunterstützung bei solchen Steigungen nicht schwächeln.
Steigungswinkel:
h
x
α
l
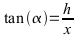
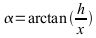
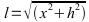
Näherung für kleine Winkel: 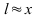 (Fehler bei 20% Steigung beträgt ca. 2%)
(Fehler bei 20% Steigung beträgt ca. 2%)
Bei einem Radgewicht von 20 kg, Eigengewicht von 80 kg, und der Näherung für kleine Winkel, dass das Steigungsverhältnis ungefähr dem Sinuswert des Winkels entspricht, ergibt sich für 100 kg bei 16% Steigung eine Hangabtriebskraft von 160N. Bei einem 26'' Rad (Radius 32,5 cm gemessen, Felge plus Mantel) ergibt sich somit ein Drehmoment von 52 Nm (160N*0,325m). Als Gegenkraft damit das Rad nicht die Schräge herunter rollt, muss entweder eine Kraft von 160N oder ein Drehmoment von 52 Nm aufgewendet werden.
Kräfte auf einer Schräge:
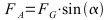
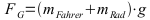
Näherung für kleine Winkel: 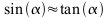 oder gleich der Steigung h/x;
oder gleich der Steigung h/x;
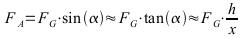 Näherung für kleine Winkel
Näherung für kleine Winkel
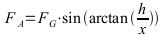 Exakte Berechnung
Exakte Berechnung
F: Kraft in N; m: Gesamtmasse in kg; g: Ortsfaktor 10 m/s2 (genauer 9,81); FA: Hangabtriebskraft; FG: Gewichtskraft;
Moment am Hebelarm:
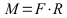
M: Moment in Nm; F: Kraft in N, R: Radius (Hebelarm senkrecht zur Kraft) in m;
|
Steigung in %, Winkelfunktionen und Abweichungen durch Näherungen |
|||||||
|
|
|
|
|
|
|
|
|
|
x in m |
h in m |
l in m |
Steigung in % |
Winkel in Grad |
Fehler l und x in % |
Hangabtriebskraft, Winkelformeln, normiert |
Fehler Hangabtriebskraft in % (Näherung) |
|
1 |
0,000 |
1,00000 |
0,0 |
0,000 |
0,000 |
0,000 |
0,000 |
|
1 |
0,010 |
1,00005 |
1,0 |
0,573 |
0,005 |
0,010 |
0,005 |
|
1 |
0,020 |
1,00020 |
2,0 |
1,146 |
0,020 |
0,020 |
0,020 |
|
1 |
0,050 |
1,00125 |
5,0 |
2,86 |
0,125 |
0,050 |
0,125 |
|
1 |
0,100 |
1,00499 |
10,0 |
5,711 |
0,499 |
0,100 |
0,499 |
|
1 |
0,200 |
1,01980 |
20,0 |
11,310 |
1,980 |
0,196 |
1,980 |
|
1 |
0,300 |
1,04403 |
30,0 |
16,699 |
4,403 |
0,287 |
4,403 |
|
1 |
0,400 |
1,07703 |
40,0 |
21,801 |
7,703 |
0,371 |
7,703 |
|
1 |
0,500 |
1,11803 |
50,0 |
26,565 |
11,803 |
0,447 |
11,803 |
|
1 |
1,000 |
1,41421 |
100,0 |
45,000 |
41,421 |
0,707 |
41,421 |
Mein einfaches Straßenmountainbike hat einen Pedalabstand von 0,17m zur Tretachse. Wenn ich mich auf die Pedale stelle, bringe ich 800N auf das Pedal. Das ergibt ungefähr 136 Nm Drehmoment auf die Pedalachse. Das Übersetzungsverhältnis beträgt 24:28 (kleinste Zähnezahl bei Pedalen gegenüber größte Zähnezahl am Hinterrad), d.h. ungefähr 0,86, und somit wären im kleinsten Gang 158,7 Nm Drehmoment auf das Hinterrad gebracht. Im größten Gang würde das Übersetzungsverhältnis 41:14, d.h. ungefähr 2,92 betragen und somit wäre das Drehmoment 46,5 Nm.
Kraft auf Pedal:
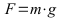 m: Masse in kg; g: Gravitationskonstante
m: Masse in kg; g: Gravitationskonstante 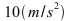
Moment am Hebelarm:
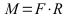
Moment auf das Hinterrad mit Getriebe-/Kettenübersetzung:
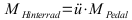
F: Kraft in N; m: Gesamtmasse in kg; g: Ortsfaktor 10 m/s2 (genauer 9,81); M: Moment in Nm; ü: Übersetzungsverhältnis (dimensionslos);
Der nachgemessene Raddurchmesser von 65cm (26''-Felge plus Radmantel) ergibt einen Hebelarm von 32,5 cm und somit wären theoretische rund 490N (160Nm/0,325m) als vorwärts treibende Kraft auf die Straße zu bringen möglich (Über Hebelvergleich plus Übersetzung wäre der Wert auch berechenbar (800N*0,17/0,325*28/24=488N). Das wäre ausreichend für fast 60% Steigung, d.h. fast 30° Steigungswinkel.
Das große Moment liegt auch nur vor wenn die Pedale eine waagrechte Position haben. Im oberen und unteren Umkehrpunkt ist das Moment praktisch Null. In einem Diagramm hätte das Moment über den Drehwinkel aufgetragen einen sinusförmigen Kurvenverlauf. Das durchschnittliche Moment wäre der Mittelwert (hier arithmetischer Mittelwert) und somit läge die durchschnittliche vorwärts treibende Kraft nur bei ca. 245N (0,5*800N*0,17/0,325*28/24=244N). Das entsprechende Drehmoment am Hinterrad betrüge 73 Nm und wäre ausreichend für rund 25% Steigung oder 14° Steigungswinkel.
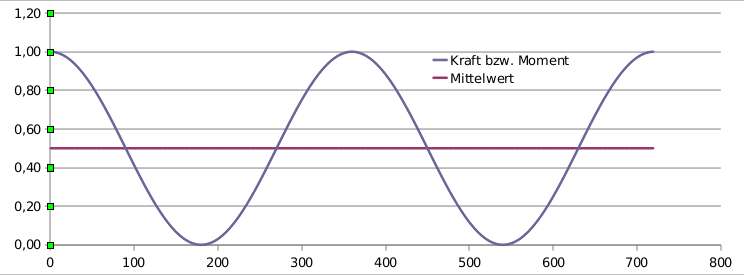
Angenäherter Verlauf der Pedalkräfte (normiert) abhängig vom Drehwinkel.
Bereits nach wenigen Pedalumdrehungen würde bei solch extremen Steigungen ein durchschnittlicher Radler in der Regel absteigen, pausieren und schieben bis es wieder flacher würde. Eine noch stärkere Untersetzung würde hier die Situation verbessern.
In der Praxis kann das maximale Moment höher werden, als das aus Gewichtskraft resultierende Moment durch Anziehen des Lenkrades mit den Armen um noch mehr Kraft auf die Pedale zu bringen. Ein normal gewichtiger Fahrer kann hier insgesamt 25% bis 50% mehr Kraft auf die Pedale durchaus schaffen. Eine andere Möglichkeit mehr Moment zu erzeugen bieten Schuhalterungen an den Pedalen um noch die Zugkraft des jeweils gegenüber Beines auszunutzen. Das bringt noch einmal 25-50% mehr Kraft für die Fortbewegung. Ein Nachteil ist, dass es etwas länger braucht im Notfall das Bein auf den Boden zu bringen, da der Fuß (bzw. Schuh) erst aus der Pedalhalterung ausgehängt (auch wenn es nur eine kleine Drehbewegung wäre) werden muss.
Bei 12% Steigung wäre das notwendige Drehmoment 40 Nm. Ein Motor mit 40Nm würde bei einem 26''-Rad maximal eine Unterstützung bis 12% Steigung ermöglichen bei reinem Motorbetrieb ohne zusätzliche Tretunterstützung. Für eine Unterstützung im Alltagsbetrieb sind das durchaus taugliche Werte für einen Motorantrieb, auch wenn obige Extrembeispiele etwas darüber liegen sollten.
Bei niedrigen Geschwindigkeiten ist die Luftkühlung für den Motor natürlich geringer, so dass das Moment nicht lange gehalten werden kann. Die Antriebskraft/das Antriebsmoment muss zum Schutz vor Überhitzung zurückgefahren werden. Bei niedrigen Geschwindigkeiten begrenzt also das maximale dauerhaft nutzbare Drehmoment die Unterstützung bei längeren Steigungsstrecken.
|
Drehmoment, Raddurchmesser und maximale Steigung |
|||
|
|
|
|
|
|
Moment in Nm |
Rad in Zoll |
Radius in cm |
Steigung in % |
|
27 |
22 |
27,7 |
9,7 |
|
27 |
26 |
32,8 |
8,2 |
|
27 |
28 |
35,3 |
7,7 |
|
40 |
22 |
27,7 |
14,4 |
|
40 |
26 |
32,8 |
12,2 |
|
40 |
28 |
35,3 |
11,3 |
Für zwei Motoren mit verschiedenen Momenten und unterschiedlichen Raddurchmesser sind in der Tabelle entsprechende maximalen Steigungen angegeben, die noch mit 100% Motorunterstützung bergauf gefahren werden könnten unter Vernachlässigung von weiteren Fahrwiderständen.
Bei den Beispielen wurde sowohl der Rechenweg über die Momente, wie auch über die Kräfte in Verbindung mit den Hebelgesetzen verwendet. Bei festem Raddurchmesser wäre eine Berechnung über die Momente der schnellere Weg.
Für die meisten Fahrer stellen Strecken mit Steigungen die größtem Ansprüche an die körperliche Fitness. An der Flachen Küste wäre durchaus möglich, dass hier der Gegenwind an erster Stelle stehen könnte.
Nachdem bei niedrigen Geschwindigkeiten das maximale Drehmoment auf Grund der Gefahr von Überhitzung nicht ausgenutzt werden kann, erscheint grundsätzlich schnell Fahren ein Ausweg aus dem Dilemma zu bieten, wenn es nicht noch eine weitere Einschränkung durch die Leistung gäbe.
Ohne Berücksichtigung einer Leistungsgrenze, wurde bei einer Motorunterstützung zusätzlich zum Pedal, der benötigte Kraftaufwand beim Treten in die Pedale, wie eine maximal 12% geringere Steigung (Steigungsabzug) erscheinen. Bei einer 16% Steigung wäre der Kraftaufwand beim Treten in die Pedale vergleichbar einer Steigung von 4% (16-12=4). Hierbei würde 75% des Moments vom Motor zugegeben.
Eine Leistungsobergrenze von 250W des Motors beschränkt die Unterstützung bei höheren Geschwindigkeiten. Bei dem Beispiel des Straßenmontainbike wird bereits in der Nähe von 10km/h auf Grund der Leistungsobergrenze das beigesteuerte Moment zurückgefahren. Mit zunehmender Geschwindigkeit nimmt der Anteil des beigesteuerten Momentes immer mehr ab. Bei 25km/h wären bis zu 3,5% Steigung oder Steigungsabzug möglich. Der Motor liefert in dem Falle maximal so viel Antrieb, dass die Steigung eine Kraft erfordert, wie für eine 3,5% weniger steile Strecke aufgewendet werden müßte. Eine Steigung von 10% würde also mit einem Kraftaufwand, wie eine Steigung von 6,5% gefahren werden. Der Motor würde in dem Beispiel ungefähr zu 1/3 unterstützen.
Berechnung der Leistungen:
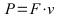
(bzw. 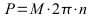 n: in U/s (Umdrehungen pro Sekunde, M: Drehmoment in Nm))
n: in U/s (Umdrehungen pro Sekunde, M: Drehmoment in Nm))
Leistung = Kraft * Geschwindigkeit, Umrechnung 1 J/s = 1 W
P: Leistung in J/s oder W; F: Kraft in N; v: Geschwindigkeit in m/s (*3,6 Umrechnung in km/h);
|
Steigungswiderstand für 100kG Gesamtgewicht |
|||||||
|
|
|
|
|
|
|
|
|
|
Steigung in % |
Steigung in Grad |
F in N |
E in Wh/km |
P in W bei 5 km/h |
P in W bei 10 km/h |
P in W bei 20 km/h |
P in W bei 50 km/h |
|
0,5 |
0,29 |
5,00 |
1,39 |
6,94 |
13,89 |
27,78 |
69,44 |
|
1 |
0,57 |
10,00 |
2,78 |
13,89 |
27,78 |
55,55 |
138,88 |
|
2 |
1,15 |
20,00 |
5,55 |
27,77 |
55,54 |
111,09 |
277,72 |
|
5 |
2,86 |
49,94 |
13,87 |
69,36 |
138,72 |
277,43 |
693,58 |
|
10 |
5,71 |
99,50 |
27,64 |
138,20 |
276,40 |
552,80 |
1.382,00 |
|
20 |
11,31 |
196,12 |
54,48 |
272,38 |
544,77 |
1.089,53 |
2.723,84 |
|
30 |
16,70 |
287,35 |
79,82 |
399,09 |
798,19 |
1.596,38 |
3.990,94 |
|
60 |
30,96 |
514,50 |
142,92 |
714,58 |
1.429,15 |
2.858,31 |
7.145,77 |
Als weitere Größe wurde in der Tabelle noch für verschiedene Steigungen die verrichtete Arbeit pro km angegeben.
Berechnung der verrichteten Arbeit:
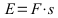
Arbeit = Weg * Strecke in Joule, Umrechnung: 3600 J = 1 Wh
E: Energie in J; F: Kraft in N,; s: Strecke in m;
Bei 10km/h wären gemäß Tabelle ungefähr bis zu 9% Steigung bei motorischer Vollunterstützung möglich. Der Motor liefert in dem Falle maximal so viel Antrieb, dass die Steigung eine Kraft erfordern würde, wie für eine 9% weniger steile Strecke aufgewendet werden müßte. Eine Steigung von 10% würde mit einem Kraftaufwand, wie eine Steigung von 1% gefahren werden. Der Motor würde ungefähr zu 90% unterstützen. Bei höheren Geschwindigkeiten, z.B. 20 km/h würde der Antrieb nur noch die Steigung etwa um 4,5 vermindern und somit betrüge die Motorunterstützung ungefähr noch 45%. Diese Zusammenhänge sollten Nutzer dieser Fortbewegungsmittel kennen.
Bei den genannten Beispielen wurden den Wirkungsgrad reduzierende Verluste zunächst weggelassen um die Sachverhalte zu vereinfachen.
Sonstiges:
Bei 25km/h wurde sich das 26''-Rad ungefähr mit 3,5 U/s bzw. 200-210 U/min drehen. Handelsübliche Gleichstrommotoren und Drehstrommotoren (Einpolmaschinen) liegen meist im Bereich von 3000-4000 U/min und benötigen daher ein Getriebe zur Herabsetzung der Drehzahl und Erhöhung des Drehmomentes.
Insgesamt überstreichen die 18 Gänge, bzw. Stufen, meines Straßenmountainbikes ein Verhältnis von 3,4 ( (41:14)/(24:28)=3,4 ). Das Gesamtverhältnis ist entscheidend, ob das Fahrrad auch wirklich breitbandig eingesetzt werden kann. Es gab Bekannte, die kauften teure Räder mit 21 und mehr Gängen, die nur einen gesamten Übersetzungsbereich von 3,0 überstrichen (0,92 bis 2,7). Der einzige Unterschied war nur eine feinere Abstufung der Gänge, der bei einem bestimmten Leistungssportprofil auch seine Berechtigung hat, bei diesen aber gar nicht zutraf. Für den normalen Nutzer (Alltagsfahrten, etwas Gelegenheitssport) ist vor allem eine möglichst große Untersetzung des kleinsten Ganges erforderlich, wenn dieser Gelände oder Straßen mit Steigungen überwinden muss.
Eine Motorunterstützung soll in der Regel das Überwinden von Höhenunterschieden erleichtern, da diese die Fahrt am häufigsten erschweren und die Fahrtzeit verlängern.
Bei hohen Geschwindigkeiten bremst vor allem der Fahrtwind. Aber bei Geschwindigkeiten bis zu einer Unterstützungsgrenze von 25 km/h fällt dieser meist nicht so stark ins Gewicht im Vergleich zu den Steigungswiderständen. Bei Gegenwind liegt die Grenze ab wann der Luftwiderstand viel Kraft kostet bei niedrigeren Geschwindigkeiten.
Wer eine Steigung hoch fährt, überwindet einen Höhenunterschied und verrichtet damit eine Hubarbeit. In der Physik gibt es den Ansatz über die Energie zur Berechnung der verrichteten mechanischen Arbeit.
Potentielle Energie:
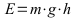
E: Energie in J oder Ws, Umrechnung J in Wh: 3600 J = 1 Wh (oder das Ergebnis in Joule durch 3600 teilen); m: Gesamtmasse in kg; g: Ortsfaktor 10 m/s2 (genauer 9,81); h: Höhendifferenz in m;
|
Hubarbeit für 100kg |
||||
|
|
|
|
|
|
|
Höhe in m |
E in Wh |
E in kJ |
E in kKal |
E in kKal bei η=22% |
|
1 |
0,3 |
0,9 |
0,2 |
1,0 |
|
3 |
0,8 |
2,8 |
0,7 |
3,0 |
|
10 |
2,8 |
9,2 |
2,2 |
10,0 |
|
50 |
13,9 |
45,8 |
10,9 |
49,8 |
|
100 |
27,8 |
91,7 |
21,9 |
99,5 |
|
1000 |
277,8 |
916,7 |
218,9 |
995,2 |
|
2000 |
555,6 |
1833,3 |
437,9 |
1990,4 |
Bei einer Gesamtmasse von 100kg werden zur Überwindung von je 100m Höhendifferenz ungefähr 30Wh Akkuenergiegehalt benötigt (27,78Wh) bei voller motorischer Unterstützung. Für die Auslegung des mitgeführten Energiespeichers spielen die Höhenunterschiede eine wesentliche Rolle.
Für eine Bergfahrt mit 1000m Höhendifferenz müßte der Akku mindestens 300-400Wh speichern. Bei einem E-Bike ohne Bremsenergierückspeisung ist zu beachten dass die Summe aller Anstiegsfahrten den Wert der Höhendifferenz 1000m nicht übersteigen darf. D.h. 600 Höhenmeter bergauf, 200m bergab und dann wieder 600m bergauf wären für das E-Bike eine Akkubelastung, als wären 1200 insgesamt Höhenmeter gefahren worden. Bei einer Einstellung von 50% Unterstützung, wäre der Akku erst nach 2000m Höhendifferenz leer.
Bei idealer Nutzbremsung, d.h. der Antrieb arbeitet als Generator, könnte die gesamte Energie wieder in den Akku zurück gespeist werden. In dem Falle würde der Berg hochgefahren bis der Akku leer wäre und anschließend zurück wieder Nutzbremsbetrieb. Am Startpunkt hätte der Akku den gleichen Ladungszustand, wie vor der Abfahrt, wenn es keine Verluste gäbe.
Da der Akku im Ladebetrieb in der Regel keine höheren Leistungsaufnahmen verträgt als bei der Leistungsabgabe, gibt es bei der Nutzbremsung auch eine Leistungsgrenze, die zu beachten ist.
Auch das Bremsmoment des Motors unterliegt physikalischen Grenzen auf Grund der Induktionsgesetze. So kann das maximale Bremsmoment im Generatorbetrieb auch nicht höher sein, als im Motorbetrieb. Bei sehr kleinen Drehzahlen des Generators wird das Bremsmoment in der Regel auch kleiner auf Grund der niedrigen Induktionsspannung, die mit der Drehzahl abnimmt. Spezielle Frequenzumrichter für Drehstrommotoren haben dieses Absinken des Momentes im Bremsbetrieb bei kleinen Drehzahlen nicht.
Zum Beispiel wären bei 10km/h bis zu 9% Steigung beim Motorbetrieb (250W) möglich. Die gleiche längere Strecke bergab gefahren würde die gesamte Energie im Nutzbremsbetrieb zurück in den Akku laden, allerdings kann die ganze Strecke mit 9% Steigung (bzw. Gefälle) bergab nicht schneller als ebenfalls 10km/h gefahren werden. Für eine nicht zu vernachlässigende Anzahl von Fahrern dürfte eine solche angepasste langsame Fahrweise bergab nicht in Frage kommen.
Bei Schussfahrten bergab werden die Geschwindigkeiten so hoch und Bremswege so lange, dass fahren mit Helm angebracht wäre. Bei niedrigen Geschwindigkeiten, d.h. Durchschnittsgeschwindigkeit 13 km/h, maximale gefahrene Geschwindigkeit 20km/h, würde eine Helmpflicht auch dem Fußgänger auferlegt werden müssen, wegen der sehr ähnlichen Risiken (Verminderung der Kopfverletzungen wenn Fußgänger stürzt oder angefahren wird).
In den Absätzen vorher beschriebene Fahrten mit maximaler Nutzbremsung auf Gefällestrecken wären auf jeden Fall weniger riskant, der Akku würde länger reichen, und auch die mechanische Bremse würde es mit weniger Abnutzung und längerer Lebensdauer der Verschleißteile danken.
Für eine Höhendifferenz von 100m werden theoretisch etwa 30 Wh (27,8 Wh, oder 0,1 MJ) benötigt. Die 0,1 MJ entsprächen ungefähr 25 Kilokalorien. Da der Mensch mit einen Wirkungsgrad von etwa 22% die Energie der Nahrung in Bewegung umsetzt, könnten hierbei rund 100 Kilokalorien abgebaut werden. Somit wäre die Energie von ¼ Liter Cola oder 4% des Tageskalorienbedarfs bei dieser Fahrt verbraucht worden.
Bei diesen Widerständen sind die Schwankungen je nach Eigenschaften des Fortbewegungsmittels, des Fahrers, des Fahrbahnbelages, des Streckenverlaufs (Anzahl und und Radien der Kurven) recht unterschiedlich. In der Literatur (leifi Physik, kreuzotter.de, usw.) werden Werte im niedrigen Bereich von 4N/kN angegeben. Diese Wiederstandswerte werden üblicherweise auf gutem Fahrtweg (ohne Schmutz und Schnee) bei Geradeausfahrt ermittelt. Für den Vergleich der Reibungsverlusten einzelnen Räder sind diese durchaus aussagekräftig.
Unter realen Bedingungen liefert ein Wert von 25N/kN (ca. 7Wh/km) Ergebnisse auf der sicheren Seite und deckt somit den additiven Mix aller Reibungsverluste gut ab (Rad/Weg und Übertragungsverluste). Ein Mountainbike mit Stollenreifen auf unsauberer Straße mit vielen Kurven kommt diesem Wert recht nahe. Ein schlammbedeckter Fahrweg, eine Schicht Sand oder Schneematsch kann höhere Werte verursachen. Ein Tourenrad oder Rennrad liegt bei den Reibungsverlusten natürlich deutlich unter diesem hohen Wert. Der Energieaufwand je Kilometer und die aufzubringende Leistung zur Überwindung der Rollwiderstände beim Fahrrad sind gemäß folgender Tabelle im Vergleich zu Steigungen und Luftwiderständen nicht hoch.
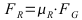
F: Kraft in N; μ: Rollreibungswert (dimensionslos), μ=0,01 entspricht 10 N/kN (bei Berechnungen besser zu händeln als Angaben in Promille); FG: Gewichtskraft in N;
|
Rollwidwerstand für 100kG (1kN) Gesamtgewicht |
||||||
|
|
|
|
|
|
|
|
|
µR in N/kN |
F in N |
E in Wh/km |
P in W bei 5 km/h |
P in W bei 10 km/h |
P in W bei 20 km/h |
P in W bei 50 km/h |
|
4 |
4 |
1,11 |
5,56 |
11,11 |
22,22 |
55,56 |
|
6 |
6 |
1,67 |
8,33 |
16,67 |
33,33 |
83,33 |
|
10 |
10 |
2,78 |
13,89 |
27,78 |
55,56 |
138,89 |
|
15 |
15 |
4,17 |
20,83 |
41,67 |
83,33 |
208,33 |
|
25 |
25 |
6,94 |
34,72 |
69,44 |
138,89 |
347,22 |
Einige Rollwiderstandswerte μR aus Physikformalsammlungen: Rad/Straße (Auto) 0,015...0,025, Rennrad 0,004, Rad 0,006, Schiene 0,002;
Der Fahrtwindeinfluß nimmt im Gegensatz zu Rollreibung stark und nicht linear mit zunehmender Geschwindigkeit zu. Der Fahrtwindwiderstand schwankt stark je nach Fortbewegungsmittel, Fahrerprofil und dessen Haltung.
Der Gegenwind auf einem Streckenstück dessen Gefälle so stark war, dass ohne Treten 30 km/h erreicht wurden, war nach dem Sturm Wiebke noch so heftig, dass ich sogar einige Meter rückwärts den Berg hochgedrückt wurde ohne in die Pedale zu treten und die Fahrt abbrach.
Luftwiderstand:
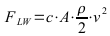
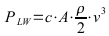
Luftdichte ρ ca. 1,1...1,3 kg/m3 je nach Luftdruck, Temperatur und Feuchtigkeit;
A: Querschittsfläche in m2; c: Luftwiderstandsbeiwert (dimensionslos); v: Geschwindigkeit in m/s; F: Kraft in N; P: Leistung in J oder W;
Beim Rad setzt sich der Luftwiderstandsbeiwert zusammen aus dem Luftwiderstandsbeiwert, der den Einfluß der Querschnittsfläche beschreibt und einem Anteil der die Länge des Fahrzeuges berücksichtigt. Für ein Alltagsrad gibt es daher Lufwiderstandsbeiwerte von bis zu 1,1 (dimensionslos), statt in Formelsammlungen für Fahrzeuge befindliche Werte von 0,4…0,9. Die Querschnittsfläche hängt dabei stark vom Fahrer und dessen Haltung ab. Die Bandbreite schwankt meistens von 0,45 bis 0,6 m2 für die Querschnittsfläche in Fahrtrichtung.
Bei 25N/kN Reibung liegt der Energiebedarf bei etwa 7 Wh/km und bei 4N/kN hätte dieser etwa 1,1 Wh/km. Ein Vergleich der Kräften und Energieaufwände zur Überwindung der Luftwiderstände verdeutlicht, dass im Bereich von mittleren Geschwindigkeiten bereits der Luftwiderstand höher als der Rollwiderstand werden kann. Gäbe es eine ein lagenwinkelabhängige Steuerung würde sich bei Gegenwind eine Motorunterstützung nicht zuschalten, aber ein eine Messung der Kraft auf die Pedale und der Geschwindigkeit berücksichtigt starke Windeinflüsse.
Bei steilen Wegstücken wird er Gegenwind glücklicherweise meistens durch den noch zu bezwingenden Hügel stark abgeschwächt und die volle Wucht des Windes trifft den Radfahrer erst im Bereich der Kuppe. Beim bergab Rollen kann ein passend starker Gegenwind durchaus schonend für die Bremse wirken.
|
Luftwiderstand für Rad mit A=0,6 und c=1,1 (ρ=1,3) |
||||
|
|
|
|
|
|
|
v in km/h |
v in m/s |
F in N |
P in W |
E in Wh/km |
|
5 |
1,39 |
0,83 |
1,15 |
0,23 |
|
10 |
2,78 |
3,31 |
9,19 |
0,92 |
|
15 |
4,17 |
7,45 |
31,03 |
2,07 |
|
20 |
5,56 |
13,24 |
73,56 |
3,68 |
|
25 |
6,94 |
20,69 |
143,67 |
5,75 |
|
30 |
8,33 |
29,79 |
248,26 |
8,28 |
|
40 |
11,11 |
52,96 |
588,48 |
14,71 |
|
50 |
13,89 |
82,75 |
1149,37 |
22,99 |
Bei einer Fahrt im Regen, wäre zusätzlich noch die Gewichtserhöhung durch das aufgenommene Wasser und die Energie für die Beschleunigung des mitgeführten Wassers berechnet werden. Ob das die Genauigkeit der Ergebnisse merklich beeinflußt oder nur „ein paar Stellen hinter dem Komma ändert“ wäre vielleicht noch eine kleine Messreihe und Thema für eine wissenschaftliche Arbeit.
Ein Fahrzeug in Bewegung stellt auch eine Form der gespeicherten Energie dar, die sogenannte kinetische Energie. Drehende Räder speichern auch Bewegungsenergie. Eine Anwendung findet dies bei Schwungradspeichern. Bei einem Fahrrad besitzen die Räder eine geringe Masse (Felgen, Speichen, Mantel und Schlauch) gegenüber dem gesamten System, so dass dieser Anteil hier vernachlässigt wird (d.h. Ergebnisse haben dadurch ca. 5% niedrigere Werte).
Kinetische Energie:
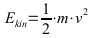
E: Energie in J; m: Masse in kg; v: Geschwindigkeit in m/s;
Zum Beispiel wird für eine Höhendifferenz von etwa 3 m einer Tiefgaragenausfahrt eine Energie von rund 1 Wh benötigt. Wird ein Anlauf vor der Steigung genommen bei dem 25-30 km/h erreicht werden, reicht der Schwung um diese Steigung ohne Schalten hoch zu radeln. Kurze steile Wegstücke können daher mit Anlauf leichter überwunden werden. Umgekehrt wird diese Geschwindigkeit auch beim Herunterrollen der Rampe erreicht. Diese Energie wird im Bremsvorgang vernichtet. Beim Nutzbremsen verursacht der Abbau von kinetischer Energie über kurze Zeit hohe Leistungsspitzen. Bei großen Beschleunigung wären diese Leistungsspitzen ebenfalls aufzuwenden.
Bei Unfällen korreliert die Stärke der Verletzung nicht wie meist angenommen mit der Geschwindigkeit, sondern mit der kinetischen Energie, die überproportional mit zunehmender Geschwindigkeit ansteigt. Bei hohen Geschwindigkeiten wäre außer einem Helm daher auch die feste Schutzkleidung von Motorradfahrern mit Beckengurt, verstärkten Kleidung im Bereich der Schultern und Beine durchaus angebracht.
Bei Unfällen als Fußgänger ohne Fahrzeugbeteiligung liegt interessanterweise der Energiebereich bei 0,5 bis 0,6 Wh. vergleichbar mit der kinetischen Energie bei 20 km/h. Beim Rennen liegt dieser vergleichbare Bereich bei 21 bis 36 km/h (100m in 17 oder 10 Sekunden). Mit den Armen abgefangen werden kann im Idealfall eine Energie, die einer Liegestütze entspricht, d.h. z.B. 100kg auf 80cm, also nur 0,3 Wh.
|
Kinetische Energie für Rad mit 100kg Gesamtgewicht: |
|||||||
|
|
|
|
|
|
|
|
|
|
v in km/h |
5 |
10 |
15 |
20 |
25 |
50 |
100 |
|
v in m/s |
1,39 |
2,78 |
4,17 |
5,56 |
6,94 |
13,89 |
27,78 |
|
E_kin in kJ |
0,10 |
0,39 |
0,87 |
1,54 |
2,41 |
9,65 |
38,58 |
|
E_kin in Wh |
0,03 |
0,11 |
0,24 |
0,43 |
0,67 |
2,68 |
10,72 |
|
|
|
|
|
|
|
|
|
|
entspricht Hub in m |
0,10 |
0,39 |
0,87 |
1,54 |
2,41 |
9,65 |
38,58 |
|
|
|
|
|
|
|
|
|
|
Bremsen |
s für Δ5km/h |
s für Δ5km/h |
s für Δ5km/h |
s für Δ5km/h |
s für Δ5km/h |
s für Δ25km/h |
s für Δ50km/h |
|
50 W |
2 |
6 |
10 |
14 |
17 |
145 |
579 |
|
100W |
1 |
3 |
5 |
7 |
9 |
72 |
289 |
|
250W |
0,4 |
1 |
2 |
3 |
3 |
29 |
116 |
|
|
|
|
|
|
|
|
|
|
Bremsen |
x für Δ5km/h |
x für Δ5km/h |
x für Δ5km/h |
x für Δ5km/h |
x für Δ5km/h |
x für Δ25km/h |
x für Δ50km/h |
|
50 W |
2 |
10 |
31 |
62 |
103 |
1575 |
12024 |
|
100W |
1,1 |
5 |
15 |
31 |
52 |
788 |
6012 |
|
250W |
0,4 |
2 |
6 |
12 |
21 |
315 |
2405 |
Die kinetischen Energie bestimmt auf ebener Stecke maßgeblich den Bremsweg und die Beschleunigungszeiten. Die Berechnung unter besonderen Randbedingungen, z.B. eine Leistungsbegrenzung ist analytisch sehr aufwendig, kann aber mit Näherungsverfahren relativ einfach bestimmt werden.
Sonstiges:
Im folgenden wird der analytische Ansatz zur Bestimmung des Kurvenverlaufs der Beschleunigungsfahrt ohne verlustbehaftete Fahrwiderstände hergeleitet. Dazu wird der Zusammenhang zunächst als Integral dargestellt.
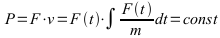
Im Prinzip wird eine Funktion gesucht. die folgende Bedingung erfüllt:
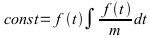
Durch Ableitung kann diese in eine Differentialgleichung umgewandelt werden in der Hoffnung, dass die Lösung einfacher würde. Ein anderer Weg geht über probieren mit verschiedenen Funktionen, Polynome, Exponentialfunktionen, Trigonometrische Funktionen, Wurzelfunktionen und sonstige Funktionen. Wer viele Ableitungen bereits selbst rechnete, fällt gegebenenfalls noch eine Rechnung mit einer Wurzelfunktionen ein und erkennt, dass diese eine mögliche Lösung sein könnte.
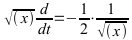
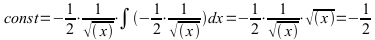
Der Ansatz zeigt, dass die grafische Lösung einen wurzelförmigen Kurvenverlauf für v(t) hätte für den Bereich mit Leistungsbegrenzung und ohne andere Fahrtwiderstände.
In der Realität sind die angegebenen Fahrwiderstände vorhanden und der theoretische Kurvenverlauf läuft exponentiell auf einen Gleichgewichtswert zu.
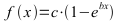
Meist kann der Verlauf ausreichend genau über diese vereinfachte Formel dargestellt werden.
Die vollständige Gleichung mit zusätzlicher Berücksichtigung der kinetischen Energie aus der Rotation wäre:
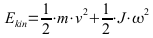
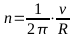 Drehzahl Rad pro Sekunde
Drehzahl Rad pro Sekunde
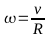 Ergebnis im Bogenmaß
Ergebnis im Bogenmaß
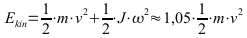
J: Trägheitsmoment des Drehkörpers, hier Vorder- und Hinterrad;
Beide Terme (translatorische und rotatorische Bewegungsenergie) haben einen quadratischen Kurvenverlauf abhängig von der Geschwindigkeit. Der Einfluß des zweiten Termes läge etwa bei 5% bei 100kg Gesamtgewicht, 20kg Radgewicht.
Das Trägheitsmoment des Hinterradnabenmotors ist auf Grund des kleineren Radius im Vergleich zur Felge deutlich geringer als man vermuten würde und würde die kinetische Energie höchstens zwischen 2-3% erhöhen.
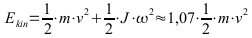
Somit läge für diesen Fall insgesamt der Einfluss des zweiten Terms bei 7 bis höchstens 8 %.
Bei den Pedal Electric Cycle (Pedelec) sind folgende Kombinationen möglich:
Elektromotorischer Hauptantrieb mit der Möglichkeit des zusätzlichen Pedalantriebs
Pedalbetriebener Hauptantrieb mit der Möglichkeit des zusätzlichen Elektromotorantriebs
Wahlweise Elektromotorantrieb oder Pedalantrieb
Jedoch sind nicht alle Kombinationen am Markt verfügbar. Häufig zu finden sind folgende Verwendung der Begriffe für Pedelec und E-Bike in Deutschland.
Pedelec als Oberbegriff für alle Mischantriebsformen Pedal und E-Motor.
Der Elektromotor von Pedelecs gibt nur ergänzend seine Leistung ab, wenn auch in die Pedale getreten wird. Bei Pedelecs ist die Motorleistung auf 250 Watt begrenzt und endet bei 25km/h. Pedelecs werden im Sinne der StVO als Fahrräder betrachtet und bedürfen keiner Zulassung, Helm und Versicherung. (StVO rechtlich als Fahrrad eingestuft)
Werden diese Kriterien nicht erfüllt spricht man meist von E-Bikes. Diese gibt es mit und ohne Pedalunterstützung, höhere Leistungen und Geschwindigkeiten. Allerdings sind dann Versicherung und Zulassung erforderlich. (StVO rechtlich als Kleinkraftrad eingestuft)
S-Pedelec für Pedelec mit mehr Motorleistung als 250W oder Motorunterstützung auch über 25km/h. Versicherung, Helm und Zulassung erforderlich. (StVO rechtlich als Kleinkraftrad eingestuft)
Sonderregelung für Antriebe bis 6km/h Anfahr-, Schiebehilfe (Nicht nur Zweiräder, keine Versicherung und Helmpflicht, z.B. für Rollstühle, E-Tretroller, Laufhilfen, Mini-Stapler, Schneefräse, Rasenmäher)
Die Normen und Gesetze der EU schreiben den Staaten keine Begriffsdefinitionen vor, aber legen für alle Staaten bindend die gleichen technischen Eigenschaften und Grenzwerte für die rechtliche Einstufung fest. Aktive E-Motorunterstützung bis 250W und 25km nur während des aktiven Pedalbetriebs wird rechtlich dem Fahrrad gleichgestellt. Somit gilt hier europaweit keine Zulassungs, Anmelde-, Versicherungs- und Helmpflicht. Alle anderen Kombinationen werden rechtlich dem Kleinkraftrad gleichgestellt. Somit gilt hier europaweit eine Anmelde-, Versicherungs- und Helmpflicht.
Den geringsten Aufwand haben natürlich Antriebssysteme, die nur Unterstützen und keine Nutzbremsung erlauben. Dazu gehören in der Regel alle Antriebe, die im Tretlagerbereich eingebaut werden. Auf Grund des Freilaufs in der Hinterradnabe können über die Kette nur Zugmomente übertragen werden. Auf der anderen Seite kann für den Antrieb die Übersetzungsänderung der Kettenschaltung am Hinterrad mit genutzt werden. Die Motoren arbeiten hier oft mit hohen Drehzahlen und großen Untersetzungen. Diese Getriebe in umgekehrter Richtung als Generator betrieben sind bei großen Untersetzungen oft sehr schwergängig und somit nicht so gut geeignet. Wenn das Hinterrad keinen Freilauf hätte würde die Kette zwangsgeführt bis zum Stillstand mitlaufen. Sollten hierbei Kleidungsteile (z.B. Hosenbein) zwischen Kette und Zahnrad geraten, würde dies eine große Verletzungsgefahr bedeuten. In dem Falle wäre der ganze Bereich mit vollschützenden Abdeckungen zu versehen.
Nutzbremsung haben einige Modelle mit Motoren in den Radnaben. Es gibt diese oft als einen relativ schnell drehenden Motor mit hohen Momenten und ein Planetengetriebe zur Untersetzung. Getriebelose und kommutatorfreie Radnabenmotoren haben keine Verschleißteile und sind somit besonders langlebige Antriebe. Die Fähigkeit der Nutzbremsung/Rekuperation/Stromrückspeisung des Antriebs hängt von der verwendeten Steuerung und Leistungselektronik ab. Wenn die Batterie noch vollgeladen ist, gibt es keine Rückspeisung, bzw. die Rückspeisung wird abgeschaltet wenn die Batterie wieder voll ist. Wenn die Batterie leer wäre kann mittels Rückspeisung diese auch wieder aufgeladen werden. Das ist auch praktisch wenn man sich ohne lange Strecke und hoher Geschwindigkeit etwas „auspowern“ möchte. Es schont die mechanische Bremse. Auf Strecken mit abwechselnd vielen Steigungen und Gefällen (im Nutzbremsbetrieb gefahren) verlängert sich die Reichweite merklich.
Als Akku wird heute bei den E-Bikes Lithiumzellen verwendet. Auf der einen Seite haben diese Zellen weniger Gewicht, kosten aber mehr als NiMh-Zellen. Auf Grund der notwendigen Schutzschaltungen bei Lithiumakkus sind diese fest verbaut und montiert am Fahrrad. Bei NiMh-Zellen (ready to use Zellen, d.h. nach 12 Monaten noch 80% der Ladung verfügbar) wäre dies weniger kritisch und könnten auch entnommen werden um z.B. in der Wohnung aufgeladen zu werden, wenn kein Anschluss in der Garage vorhanden wäre. Das Gewicht wäre in dem Falle etwa 0,3 kg für 30Wh und 3kg für 300Wh. Vielleicht findet sich noch ein Hersteller, der nur einen kleinen Li-Akku einbaut, mit der Option als Ergänzungspack einen NiMh-Block anzuschließen für mehr Gesamtenergie beim Fahren oder auch nur zum Laden des kleinen eingebauten Li-Akkus.
Selbst besitze ich noch kein E-Bike/Pedelec und bevorzuge es noch komplett selbst in die Pedale zu treten. Wenn ich mir ein E-Bike/Pedelec kaufen sollte, dann käme für mich nur ein Modell mit Nutzbremse (Rekuperation) in Frage. Tendieren würde ich dabei eher zum Pedelec, wegen der größeren Flexibilität (kein Helm, z.B. wohin mit dem Helm am Bahnhof).
Es gibt im Internet genügend Seiten mit Vergleichen der Vor- und Nachteile von verschiedenen Modellen, die über Suchmaschinen leicht zu finden sind. Einige mir dort nicht vorhandene oder nur selten aufgeführte Aspekte habe ich hier gesammelt. Es gibt auch Sonderbauformen, die die aufgeführten Vor- oder Nachteile in stärkerer oder schwächer Form enthalten.
|
Vergleich der Antriebsarten |
|||
|
Eigenschaften |
Mittenmotor |
Vorderradmotor |
Hinterradmotor |
|
Rahmen: |
Benötigt eigens konstruierten Rahmen im Bereich der Tretlager. |
Keine Änderung und kann in die meisten Rahmen eingebaut werden. |
Keine Änderung und kann in die meisten Rahmen eingebaut werden. |
|
Bausätze: |
Es gibt Bausätze, bei denen muß der Rahmen bearbeitet werden. |
Ja, gbt es. |
Ja, gibt es. |
|
Motorgewicht: |
3-4 kg |
3kg (Getriebemotor) 3,5-5kg (Getriebeloser Motor) |
3kg (Getriebemotor) 3,5-5kg (Getriebeloser Motor) |
|
max. Drehmomente: |
27-60 Nm |
27-60 Nm |
27-60 Nm |
|
Schwerpunktlage: |
Liegt tiefer als bei Radnabenmotoren |
Liegt höher als bei Mittenmotoren. |
Liegt höher als bei Mittenmotoren. |
|
Ruperation / Nutzbremsbetrieb |
Nicht möglich, wegen Freilauf. (Freilauf der Kettenschaltung) |
Nicht möglich bei Motoren mit Freilauf. Ja, ist möglich, aber auf dem Markt kaum erhältlich. |
Nicht möglich bei Motoren mit Freilauf. Ja, gibt es auf dem Markt. (meist auf max. 100W begrenzt) |
|
Verschleiß Kette |
Erhöht den Verschleiß der Kette, da der Antrieb auf die Kette wirkt. |
Kein Mehrverschleiß der Kette.
|
Kein Mehrverschleiß der Kette. |
|
Verschleiß Zahnkränze |
Erhöht den Verschleiß der Zahnkränze, da der Antrieb auf die Kette wirkt. |
Kein Mehrverschleiß der Zahnkränze. |
Kein Mehrverschleiß der Zahnkränze. |
|
Mitnutzung von Übersetzungen |
Ja, da der Antrieb auf die Kette wirkt bzw. auf die Tretachse. |
Nein, da der Antrieb direkt auf das Rad wirkt.
|
In der Regel Nein, da der Antrieb direkt auf das Rad wirkt. Es gibt aber Varianten mit integrierten Nabengetriebe, die die Übersetzung mit nutzen. |
|
Fail safe Optionen in Verbindung mit Verschleiß |
Kette, Zahnkränze, bei Ausfall, nur noch Schieben möglich. |
Anfahrhilfe bis 6km sofern vorhanden kann noch verwendet werden. |
Anfahrhilfe bis 6km sofern vorhanden kann noch verwendet werden. Wenn Übersetzungen mit genutzt werden, nur Schieben möglich. |
|
Fail safe Optionen in Verbindung mit Motorausfall oder Steuerungsausfall. |
Bei einigen Modellen kann auch der Tretantrieb nicht mehr nutzbar sein. |
Fortsetzung der Fahrt mit Tretantrieb ohne Motorunterstützung. |
Fortsetzung der Fahrt mit Tretantrieb ohne Motorunterstützung. Wenn Übersetzungen mit genutzt werden, nur Schieben möglich. |
|
Mitnahme Antriebskomponenten in ein anderes Rad. |
In der Regel nicht möglich. |
Meistens möglich Komponenten in ein anderes normales Rad einzubauen für versierte Bastler. |
Meistens möglich Komponenten in ein anderes normales Rad einzubauen für versierte Bastler. |
|
Weiternutzung als nur normales Rad ohne Antrieb. |
Bedingt möglich. |
Normale Hinterradfelge ohne Motor einbauen und E-Teile abmontieren. |
Normale Hinterradfelge ohne Motor einbauen und E-Teile abmontieren. |
|
Umbau auf anderes Produkt anderer Hersteller. |
Rahmen in der Regel so spezifisch, dass nur Produkte des Herstellers verwendet werden können, solange diese noch erhältlich sind. |
In der Regel Produkte anderer Hersteller einbaubar. |
In der Regel Produkte anderer Hersteller einbaubar. |
|
Ggf. eingebaute Sensoren: |
Temperatursensor, Hallsensor |
Temperatursensor, Hallsensor |
Temperatursensor, Hallsensor |
|
Spannungsbereiche: |
erhältlich für 24-48V |
erhältlich für 24-48V |
erhältlich für 24-48V |
|
Verschiebung Optimumspunkt: |
Verschiebung, da Übersetzungen mit genutzt werden. |
Nicht verschiebbar. |
a) Nicht verschiebbar. b) Verschiebbar bei Motoren mit speziellen Zusatzwicklungen oder Steuerung der Polpaarzahl. c)Verschiebung, wenn Übersetzungen (z.B. spez. integr. Nabenschaltung) mit genutzt werden. |
Die Verläufe von Wirkungsgradkennlinien sind abhängig von der Drehzahl und vom abgegebenen Drehmoment. Diese haben im Arbeitsbereich ein Maximum und fallen auf beiden Seiten einen abfallenden Kurvenverlauf.
Die Diagramme werden entweder bei bestimmten Nenngrößen ermittelt oder es werden jeweils die optimalen Punkte ähnlich einer Wurzelortskurve aufgetragen. Ausführlicher und aussagekräftiger wäre ein zweidimensionales Kennlinienfeld mit Höhenliniendarstellung für den Wirkungsgrad (Muscheldiagramm, Verbrauchskennlinienfeld).
Wenn ein solches Diagramm eines konventionellen Verbrennungsmotors mit dem eines Elektromotorantriebes verglichen werden würde, fiele auf daß der Kurvenverlauf des E-Antriebs fiel flacher verläuft. Dieser Vorteil wird beim Hybridantrieb ausgenutzt für bessere Wirkungsgrade bei einem üblichen Fahrbelastungsmix.
Einflußgrößen auf den Wirkungsgrad haben in der Regel folgende Effekte ohne Anspruch auf Vollständigkeit:
Große Momente benötigen einen großen Strom durch die Wicklungen. Die ohmschen Verluste in den Wicklungen steigen quadratisch mit dem Strom an. Die maximale Permeabilität der Materialien setzt auch Grenzen für erreichbaren Drehmomente eines Motors.
Hohe Drehzahlen benötigt hohe Frequenzen bei der Ansteuerung der einzelnen Wicklungen. Es nehmen hier die Verluste zu durch Magnetisierung, Wirbelströme, Skineffekt und Induktivitäten (Blindleistung, Blindwiderstände) zu. Luftwiderstände im Motor nehme auch überproportional zu.
Bei kleinen Drehzahlen und Momenten wird das Verhältnis von abgegebener Nutzleistung zu den Mindestverlusten ungünstiger. Hierzu zählen z.B. Hystereseverluste (auch Restmagnetismus) und Reibungsverluste.
Das zweidimensionale Kennlinienfeld des Rennrad-, City- oder Mountain-Radlers würde unterschiedlich aussehen. Die Kennlinienfelder der Antriebe auf dem Markt, die viel über die Dimensionierung des Herstellers erzählen würden, sind leider nicht verfügbar. Somit muss sich der Kunde auf seinen subjektiven Eindruck bei seinen Testfahrten verlassen. Ein erfahrener Händler wird in der Regel bei der Auswahl unterstützen, so dass sich die Zahl der Testfahrten in Grenzen halten wird.
Die folgende Skizze zeigt grob den prinzipiellen Unterschied des Verbrauchskennfeld, auch Muscheldiagramm oder Wirkungsgradkennfeld eines Verbrennungsmotors (linke Skizze) zu einem Elektromotor (rechte Skizze):
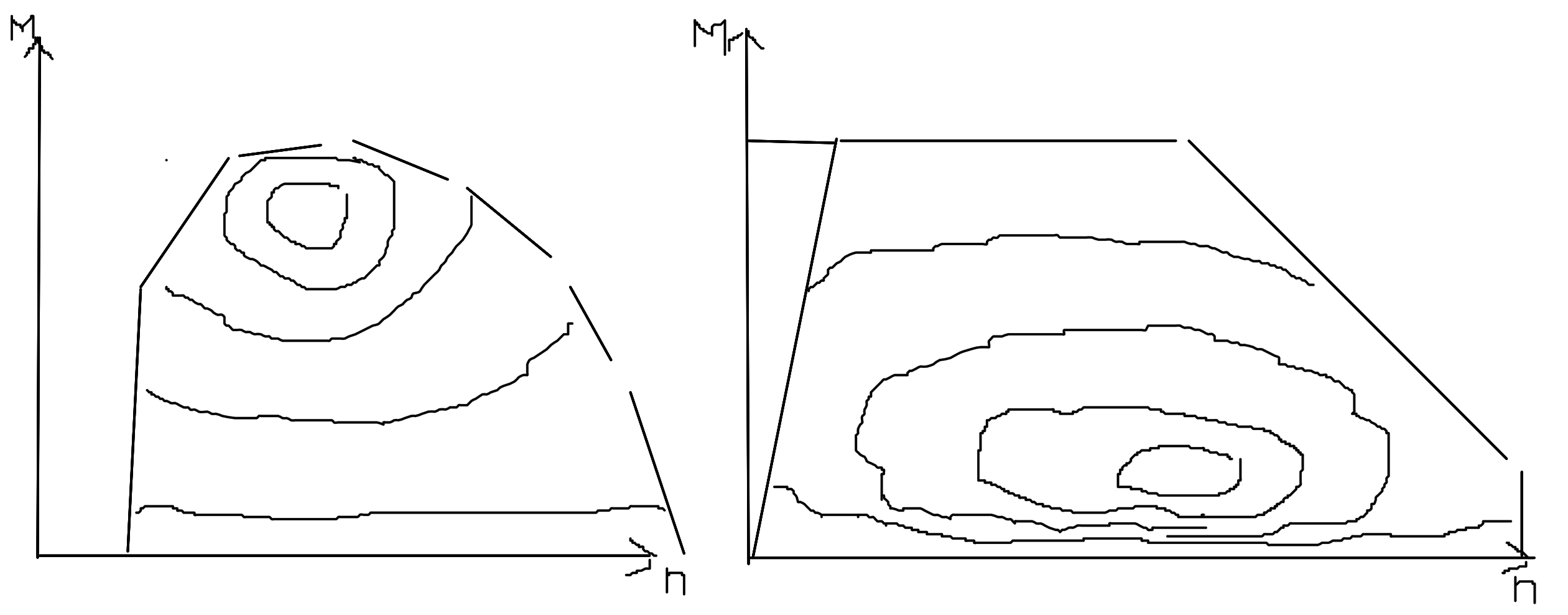
Gute Simulationen haben solche Wirkungsgradkennfelder des Gesamtsystems hinterlegt. Mittels dieser Kenntnisse kann umgekehrt natürlich auch vor einem praktischen Test eine Strecke (auch sehr lange Strecken wie auch Rundstrecken) bzw. ein Streckenmix zusammengestellt werden um ein bestimmtes System besser als ein anderes System abschneiden zu lassen. Auch Normen und Fachzeitschriften sind vor solchen Einflüssen nicht gefeit.
Der Pedelec-Fahrer sollte sich bewußt sein, dass viel fahren im ungünstigen Wirkungsgradbereich schneller die Batterie leert. Bei vielen Antrieben der beginnt der wirkungsgradoptimale Bereich in der Nähe von 13 km/h (oder beginnt ab der Geschwindigkeit und verläuft relativ flach bis ca. 20 km/h für Pedelecs bis 25 km/h Unterstützungsgeschwindigkeit), wenn Momente des Antriebs abgefordert werden. Würde der Motor zusätzlich noch im Bereich von 1/7...1/4 des maximalen Nennmomentes betrieben, wäre der Wirkungsgrad noch besser (weil noch näher am Optimum). Ein Hilfsantrieb, der die Übersetzung einer Gangschaltung teilweise mit nutzen kann, hat hier einen kleinen Vorteil, da sich der optimale Punkt bzw. Bereich entsprechend des geänderten Übersetzungsverhältnisses verschiebt. Allerdings sind hier die Übersetzungskomponenten einem höheren Verschleiß ausgesetzt.
Mit einer Tabellekalkulationsanwendung (OpenOffice Calc, MS EXCEL, Gnumeric, LibreOffice) r lassen sich die Beschleunigungsfahrten relativ einfach berechnen. Bei Verwendung einer Tabellenkalkulationsanwendung steigen die Fehler bei zu großen Schritten auf der anderen Seite bei zu kleinen Schritten wird die Tabelle sehr groß und ist kaum noch zu händeln. Hier bewährt hat sich für die meisten Berechnungen eine Tabelle mit einer Schrittweite von 0,1 Sekunden. Bei der Leistung P gibt es dabei einen kleinen Überschwinger, der das Gesamtergebnis im Wesentlichen nicht beeinflußt.
Bei Umsetzung der Bewegungsgleichungen in ein numerisches Verfahren müssen Zirkelschlüsse vermieden werden. Somit werden nach Möglichkeit die die Ergebnisse jeweils aus Werten der vorherigen Zeile berechnet.
Bewegungsgleichungen für F(t): Konstanter Wert; a: Beschleunigung in m/s2:
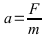
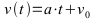
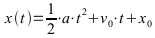
Die Formeln können auch über die Integration hergeleitet werden.
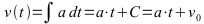
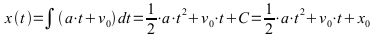
Für zeitlich nicht konstante Beschleunigung werden die Integrale oft sehr schwierig analytisch zu lösen. Umgehen läßt sich die Hürde mit numerischen Verfahren, die im folgenden angewendet werden.
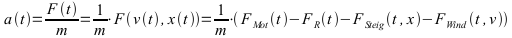
Obiges wäre eine mögliche Formel für die meisten Abhängigkeiten.
Zur Integration wird hier die Rechteckregel zum Teil vermischt mit der Trapezregel verwendet.
Numerischer Aufbau:
Step 1a:
Bedingung 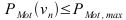
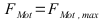
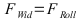
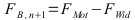
Bedingung, wenn beim nächsten Schritt 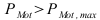
Mit 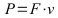 bzw:
bzw: 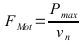
Die Differenz der Kräfte des Antriebes abzüglich der Widerstände bleibt für die Beschleunigung übrig.

Step 1b:
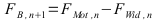
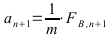
Step 2:
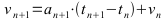
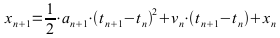
Step 1a: Kräfte berechnen mit Fallunterscheidung
Step 1b: Beschleunigung berechnen
Step 2: Geschwindigkeit und zurückgelegte Strecke berechen.
usw.
Das folgende Schaubild zeigt einen schleifenfreien Aufbau des Algorithmus von Zeitschritt „n“ zum nächsten Zeitschritt „n+1“. Es empfiehlt sich ein solches Schaubild zu entwerfen, um Indizierungsfehler zu vermeiden.
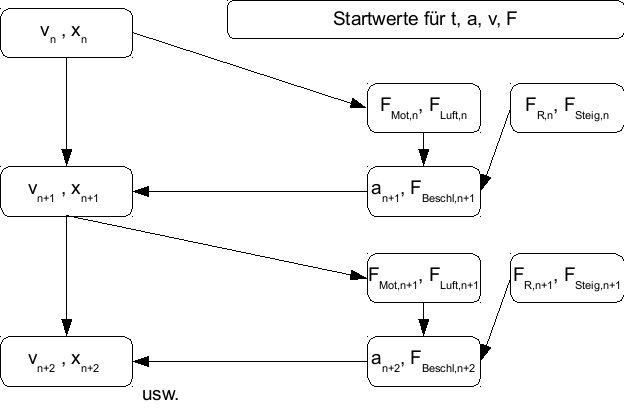
Dies wird Schritt für Schritt für jede Zeile ausgeführt. Hier beim numerischen Verfahren bestehen der verlustbehaftete Fahrwiderstand nur aus der die Rollreibung. In der folgenden Tabelle wurde die Beschleunigung ohne Fahrwiderstandsverluste ausgeführt.
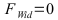
|
t |
X |
v |
v km/h |
a |
F_Mot |
P_Mot |
Pmax |
Fmax |
Gas |
|
-0,1 |
0,00 |
0,00 |
0,00 |
0,00 |
0,0 |
0,0 |
250 |
100 |
0 |
|
0,0 |
0,00 |
0,00 |
0,00 |
1,00 |
100,0 |
0,0 |
250 |
100 |
1 |
|
0,1 |
0,01 |
0,10 |
0,36 |
1,00 |
100,0 |
10,0 |
250 |
100 |
1 |
|
0,2 |
0,02 |
0,20 |
0,72 |
1,00 |
100,0 |
20,0 |
250 |
100 |
1 |
|
0,3 |
0,05 |
0,30 |
1,08 |
1,00 |
100,0 |
30,0 |
250 |
100 |
1 |
|
0,4 |
0,08 |
0,40 |
1,44 |
1,00 |
100,0 |
40,0 |
250 |
100 |
1 |
|
0,5 |
0,13 |
0,50 |
1,80 |
1,00 |
100,0 |
50,0 |
250 |
100 |
1 |
|
1,0 |
0,50 |
1,00 |
3,60 |
1,00 |
100,0 |
100,0 |
250 |
100 |
1 |
|
2,0 |
2,00 |
2,00 |
7,20 |
1,00 |
100,0 |
200,0 |
250 |
100 |
1 |
|
3,0 |
4,50 |
2,98 |
10,72 |
0,87 |
86,5 |
257,7 |
250 |
100 |
1 |
|
4,0 |
7,88 |
3,75 |
13,49 |
0,68 |
67,9 |
254,7 |
250 |
100 |
1 |
|
5,0 |
11,95 |
4,38 |
15,76 |
0,58 |
57,9 |
253,4 |
250 |
100 |
1 |
|
10,0 |
39,98 |
6,67 |
24,01 |
0,38 |
37,7 |
251,4 |
250 |
100 |
1 |
|
15,0 |
77,68 |
8,35 |
30,05 |
0,30 |
30,1 |
250,9 |
250 |
100 |
1 |
|
20,0 |
122,97 |
9,74 |
35,05 |
0,26 |
25,7 |
250,7 |
250 |
100 |
1 |
|
25,0 |
174,74 |
10,95 |
39,41 |
0,23 |
22,9 |
250,5 |
250 |
100 |
1 |
|
30,0 |
231,05 |
12,02 |
43,27 |
0,21 |
20,8 |
250,4 |
250 |
100 |
1 |
|
35,0 |
293,68 |
13,02 |
46,87 |
0,19 |
19,2 |
250,4 |
250 |
100 |
1 |
|
40,0 |
361,12 |
13,95 |
50,21 |
0,18 |
17,9 |
250,3 |
250 |
100 |
1 |
|
45,0 |
433,06 |
14,82 |
53,35 |
0,17 |
16,9 |
250,3 |
250 |
100 |
1 |
|
50,0 |
509,23 |
15,64 |
56,31 |
0,16 |
16,0 |
250,3 |
250 |
100 |
1 |
|
55,0 |
589,40 |
16,42 |
59,12 |
0,15 |
15,2 |
250,2 |
250 |
100 |
1 |
|
60,0 |
673,39 |
17,17 |
61,80 |
0,15 |
14,6 |
250,2 |
250 |
100 |
1 |
Hinterlegt in den Zellen sind folgende Formeln:
|
t |
X |
v |
v km/h |
a |
F |
P |
Pmax |
Fmax |
Gas |
|
-0,1 |
0,00 |
0,00 |
=C4*3,6 |
=F4/100 |
0,0 |
=F4*C4 |
250 |
100 |
0 |
|
=A4+0,1 |
=0,5*E4*(A5-A4)^2+C4*(A5-A4)+B4 |
=E4*(A5-A4)+C4 |
=C5*3,6 |
=F5/100 |
=IF(C4<N4/O4;P5*O5;N4/C4*P5) |
=F5*C5 |
=H4 |
=I4 |
1 |
|
=A5+0,1 |
=0,5*E5*(A6-A5)^2+C5*(A6-A5)+B5 |
=E5*(A6-A5)+C5 |
=C6*3,6 |
=F6/100 |
=IF(C5<N5/O5;P6*O6;N5/C5*P6) |
=F6*C6 |
=H5 |
=I5 |
1 |
Anbei noch eine Methode um nur die Zeilen jeder vollen Sekunde aus der langen Tabelle zu selektieren (Funktionen: engl: vlookup, deutsch: sverweis):
|
t |
v m/s |
v km/h |
|
0 |
=VLOOKUP(L4;A$4:D$300;3;1) |
=VLOOKUP(L4;A$4:D$300;4;1) |
|
=L4+1 |
=VLOOKUP(L5;A$4:D$300;3;1) |
=VLOOKUP(L5;A$4:D$300;4;1) |
|
=L5+1 |
=VLOOKUP(L6;A$4:D$300;3;1) |
=VLOOKUP(L6;A$4:D$300;4;1) |
|
=L6+1 |
=VLOOKUP(L7;A$4:D$300;3;1) |
=VLOOKUP(L7;A$4:D$300;4;1) |
Das ganze ergibt folgende Wertetabelle und Graphen:
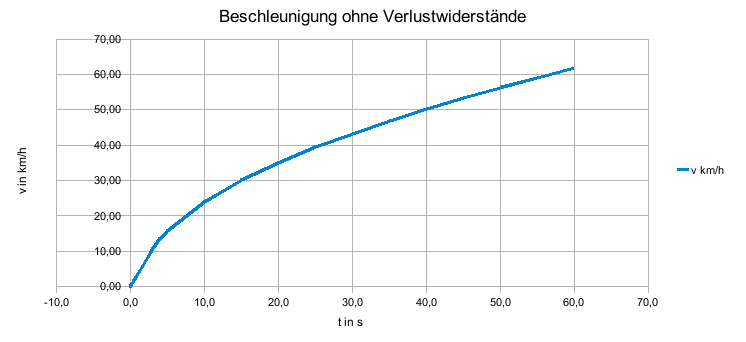
x-Achse: Zeit in s; y-Achse: Geschwindigkeit in km/h
Beim Kurvenverlauf ist der leichte Knick zu erkennen, ab dem der lineare Verlauf in den wurzelförmigen Verlauf im Diagramm übergeht.
Die weiteren Fahrwiderstände lassen sich für eine erweiterte Simulation einfach ergänzen, in dem diese in einer weiteren Spalte berechnet werden und der Wert in der Spalte „F“ abgezogen werden.
Bei der numerischen Berechnung wurde nur das vorhanden sein eines Rollwiderstandes angenommen.
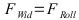
|
t |
X |
v |
v km/h |
a |
F_B Rest |
F_Roll |
F_Mot |
P |
Pmax |
Fmax |
Gas |
|
-0,1 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,0 |
0,0 |
0,0 |
250 |
100 |
0 |
|
0,0 |
0,00 |
0,00 |
0,00 |
0,90 |
90,00 |
10,0 |
100,0 |
0,0 |
250 |
100 |
1 |
|
0,1 |
0,00 |
0,09 |
0,32 |
0,90 |
90,00 |
10,0 |
100,0 |
9,0 |
250 |
100 |
1 |
|
0,2 |
0,02 |
0,18 |
0,65 |
0,90 |
90,00 |
10,0 |
100,0 |
18,0 |
250 |
100 |
1 |
|
0,3 |
0,04 |
0,27 |
0,97 |
0,90 |
90,00 |
10,0 |
100,0 |
27,0 |
250 |
100 |
1 |
|
0,4 |
0,07 |
0,36 |
1,30 |
0,90 |
90,00 |
10,0 |
100,0 |
36,0 |
250 |
100 |
1 |
|
0,5 |
0,11 |
0,45 |
1,62 |
0,90 |
90,00 |
10,0 |
100,0 |
45,0 |
250 |
100 |
1 |
|
1,0 |
0,45 |
0,90 |
3,24 |
0,90 |
90,00 |
10,0 |
100,0 |
90,0 |
250 |
100 |
1 |
|
2,0 |
1,80 |
1,80 |
6,48 |
0,90 |
90,00 |
10,0 |
100,0 |
180,0 |
250 |
100 |
1 |
|
3,0 |
4,05 |
2,70 |
9,72 |
0,86 |
85,79 |
10,0 |
95,8 |
258,5 |
250 |
100 |
1 |
|
4,0 |
7,14 |
3,44 |
12,40 |
0,64 |
63,99 |
10,0 |
74,0 |
254,8 |
250 |
100 |
1 |
|
5,0 |
10,89 |
4,03 |
14,51 |
0,53 |
52,89 |
10,0 |
62,9 |
253,4 |
250 |
100 |
1 |
|
10,0 |
36,47 |
6,04 |
21,73 |
0,32 |
31,64 |
10,0 |
41,6 |
251,3 |
250 |
100 |
1 |
|
15,0 |
70,24 |
7,40 |
26,66 |
0,24 |
23,87 |
10,0 |
33,9 |
250,8 |
250 |
100 |
1 |
|
20,0 |
110,05 |
8,48 |
30,54 |
0,20 |
19,54 |
10,0 |
29,5 |
250,6 |
250 |
100 |
1 |
|
25,0 |
154,78 |
9,39 |
33,79 |
0,17 |
16,68 |
10,0 |
26,7 |
250,4 |
250 |
100 |
1 |
|
30,0 |
202,69 |
10,15 |
36,55 |
0,15 |
14,66 |
10,0 |
24,7 |
250,4 |
250 |
100 |
1 |
|
35,0 |
255,22 |
10,85 |
39,04 |
0,13 |
13,08 |
10,0 |
23,1 |
250,3 |
250 |
100 |
1 |
|
40,0 |
311,03 |
11,47 |
41,28 |
0,12 |
11,82 |
10,0 |
21,8 |
250,3 |
250 |
100 |
1 |
|
45,0 |
369,80 |
12,03 |
43,32 |
0,11 |
10,80 |
10,0 |
20,8 |
250,2 |
250 |
100 |
1 |
|
50,0 |
431,27 |
12,55 |
45,18 |
0,10 |
9,94 |
10,0 |
19,9 |
250,2 |
250 |
100 |
1 |
|
55,0 |
495,24 |
13,03 |
46,90 |
0,09 |
9,20 |
10,0 |
19,2 |
250,2 |
250 |
100 |
1 |
|
60,0 |
561,51 |
13,47 |
48,50 |
0,09 |
8,57 |
10,0 |
18,6 |
250,2 |
250 |
100 |
1 |
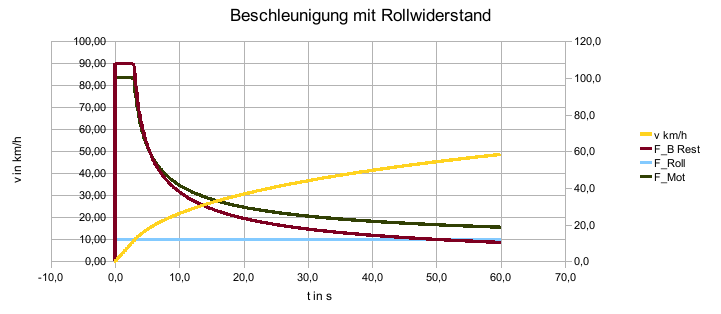
In dem Diagramm ist die Stagnation auf einen Grenzwert noch nicht zu erkennen. Bei einer Rollreibung von 10 N läge dieser bei 90 km/h und bei einer Rollreibung von 25 N läge dieser bei 36 km/h. Beim Kurvenverlauf ist der leichte Knick zu erkennen, ab dem der lineare Verlauf in eine nichtlinearen Kurvenverlauf übergeht.
Bei der numerischen Berechnung wurde nur das vorhanden sein eines Steigungswiderstandes angenommen.
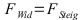
|
t |
X |
v |
v km/h |
a |
F_B Rest |
F_Steig |
F_Mot |
P |
Pmax |
Fmax |
Gas |
|
-0,1 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,0 |
0,0 |
0,0 |
250 |
100 |
0 |
|
0,0 |
0,00 |
0,00 |
0,00 |
0,50 |
50,00 |
50,0 |
100,0 |
0,0 |
250 |
100 |
1 |
|
0,1 |
0,00 |
0,05 |
0,18 |
0,50 |
50,00 |
50,0 |
100,0 |
5,0 |
250 |
100 |
1 |
|
0,2 |
0,01 |
0,10 |
0,36 |
0,50 |
50,00 |
50,0 |
100,0 |
10,0 |
250 |
100 |
1 |
|
0,3 |
0,02 |
0,15 |
0,54 |
0,50 |
50,00 |
50,0 |
100,0 |
15,0 |
250 |
100 |
1 |
|
0,4 |
0,04 |
0,20 |
0,72 |
0,50 |
50,00 |
50,0 |
100,0 |
20,0 |
250 |
100 |
1 |
|
0,5 |
0,06 |
0,25 |
0,90 |
0,50 |
50,00 |
50,0 |
100,0 |
25,0 |
250 |
100 |
1 |
|
1,0 |
0,25 |
0,50 |
1,80 |
0,50 |
50,00 |
50,0 |
100,0 |
50,0 |
250 |
100 |
1 |
|
2,0 |
1,00 |
1,00 |
3,60 |
0,50 |
50,00 |
50,0 |
100,0 |
100,0 |
250 |
100 |
1 |
|
3,0 |
2,25 |
1,50 |
5,40 |
0,50 |
50,00 |
50,0 |
100,0 |
150,0 |
250 |
100 |
1 |
|
4,0 |
4,00 |
2,00 |
7,20 |
0,50 |
50,00 |
50,0 |
100,0 |
200,0 |
250 |
100 |
1 |
|
5,0 |
6,25 |
2,50 |
9,00 |
0,50 |
50,00 |
50,0 |
100,0 |
250,0 |
250 |
100 |
1 |
|
10,0 |
22,87 |
3,87 |
13,92 |
0,15 |
14,89 |
50,0 |
64,9 |
251,0 |
250 |
100 |
1 |
|
15,0 |
43,67 |
4,39 |
15,80 |
0,07 |
7,06 |
50,0 |
57,1 |
250,4 |
250 |
100 |
1 |
|
20,0 |
66,33 |
4,65 |
16,74 |
0,04 |
3,79 |
50,0 |
53,8 |
250,2 |
250 |
100 |
1 |
|
25,0 |
89,99 |
4,80 |
17,27 |
0,02 |
2,15 |
50,0 |
52,1 |
250,1 |
250 |
100 |
1 |
|
30,0 |
113,71 |
4,88 |
17,56 |
0,01 |
1,26 |
50,0 |
51,3 |
250,1 |
250 |
100 |
1 |
|
35,0 |
138,23 |
4,93 |
17,74 |
0,01 |
0,74 |
50,0 |
50,7 |
250,0 |
250 |
100 |
1 |
|
40,0 |
162,95 |
4,96 |
17,84 |
0,00 |
0,44 |
50,0 |
50,4 |
250,0 |
250 |
100 |
1 |
|
45,0 |
187,78 |
4,97 |
17,91 |
0,00 |
0,26 |
50,0 |
50,3 |
250,0 |
250 |
100 |
1 |
|
50,0 |
212,68 |
4,98 |
17,94 |
0,00 |
0,16 |
50,0 |
50,2 |
250,0 |
250 |
100 |
1 |
|
55,0 |
237,62 |
4,99 |
17,97 |
0,00 |
0,10 |
50,0 |
50,1 |
250,0 |
250 |
100 |
1 |
|
60,0 |
262,58 |
4,99 |
17,98 |
0,00 |
0,06 |
50,0 |
50,1 |
250,0 |
250 |
100 |
1 |
In der Tabelle oder dem Diagramm ist die Stagnation auf einen Grenzwert von 18 km/h gut zu erkennen. Hier wurde vereinfacht vorherige Tabellenmethode zur Berechnung übernommen, indem 5% Steigung einer Gegenkraft von 50 N entspricht. Anzumerken sei, dass der gleiche Verlauf sich ergäbe bei einer Rollreibung von 50 N.
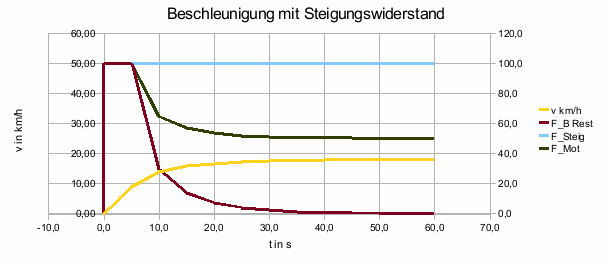
Bei der numerischen Berechnung wurde nur das vorhanden sein eines Steigungswiderstandes angenommen.
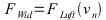
|
t |
X |
v |
v km/h |
a |
F_B Rest |
F_Luft |
F_Mot |
P |
Pmax |
Fmax |
Gas |
|
-0,1 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,0 |
0,0 |
0,0 |
250 |
100 |
0 |
|
0,0 |
0,00 |
0,00 |
0,00 |
1,00 |
100,00 |
0,0 |
100,0 |
0,0 |
250 |
100 |
1 |
|
0,1 |
0,01 |
0,10 |
0,36 |
1,00 |
100,00 |
0,0 |
100,0 |
10,0 |
250 |
100 |
1 |
|
0,2 |
0,02 |
0,20 |
0,72 |
1,00 |
100,00 |
0,0 |
100,0 |
20,0 |
250 |
100 |
1 |
|
0,3 |
0,04 |
0,30 |
1,08 |
1,00 |
99,98 |
0,0 |
100,0 |
30,0 |
250 |
100 |
1 |
|
0,4 |
0,08 |
0,40 |
1,44 |
1,00 |
99,96 |
0,0 |
100,0 |
40,0 |
250 |
100 |
1 |
|
0,5 |
0,12 |
0,50 |
1,80 |
1,00 |
99,93 |
0,1 |
100,0 |
50,0 |
250 |
100 |
1 |
|
1,0 |
0,50 |
1,00 |
3,60 |
1,00 |
99,65 |
0,3 |
100,0 |
99,9 |
250 |
100 |
1 |
|
2,0 |
2,00 |
1,99 |
7,17 |
0,98 |
98,46 |
1,5 |
100,0 |
199,1 |
250 |
100 |
1 |
|
3,0 |
4,47 |
2,95 |
10,61 |
0,84 |
83,87 |
3,5 |
87,4 |
257,6 |
250 |
100 |
1 |
|
4,0 |
7,81 |
3,68 |
13,26 |
0,63 |
63,48 |
5,6 |
69,1 |
254,5 |
250 |
100 |
1 |
|
5,0 |
11,79 |
4,26 |
15,34 |
0,52 |
51,81 |
7,6 |
59,4 |
253,1 |
250 |
100 |
1 |
|
10,0 |
38,20 |
6,09 |
21,91 |
0,25 |
25,48 |
15,8 |
41,2 |
251,1 |
250 |
100 |
1 |
|
15,0 |
71,29 |
7,06 |
25,40 |
0,14 |
14,24 |
21,3 |
35,5 |
250,5 |
250 |
100 |
1 |
|
20,0 |
108,06 |
7,60 |
27,37 |
0,08 |
8,16 |
24,8 |
32,9 |
250,3 |
250 |
100 |
1 |
|
25,0 |
146,94 |
7,92 |
28,51 |
0,05 |
4,71 |
26,9 |
31,6 |
250,2 |
250 |
100 |
1 |
|
30,0 |
186,22 |
8,10 |
29,16 |
0,03 |
2,76 |
28,1 |
30,9 |
250,1 |
250 |
100 |
1 |
|
35,0 |
227,01 |
8,21 |
29,54 |
0,02 |
1,60 |
28,9 |
30,5 |
250,0 |
250 |
100 |
1 |
|
40,0 |
268,21 |
8,27 |
29,76 |
0,01 |
0,92 |
29,3 |
30,2 |
250,0 |
250 |
100 |
1 |
|
45,0 |
309,65 |
8,30 |
29,89 |
0,01 |
0,53 |
29,6 |
30,1 |
250,0 |
250 |
100 |
1 |
|
50,0 |
351,22 |
8,32 |
29,97 |
0,00 |
0,31 |
29,7 |
30,0 |
250,0 |
250 |
100 |
1 |
|
55,0 |
392,87 |
8,34 |
30,01 |
0,00 |
0,18 |
29,8 |
30,0 |
250,0 |
250 |
100 |
1 |
|
60,0 |
434,57 |
8,34 |
30,04 |
0,00 |
0,10 |
29,9 |
30,0 |
250,0 |
250 |
100 |
1 |
Für den Luftwiderstand wurde z.B. in Zelle C5 F_Luft folgende Formel und Werte verwendet: =0,5*1,3*0,6*1,1*C4^2
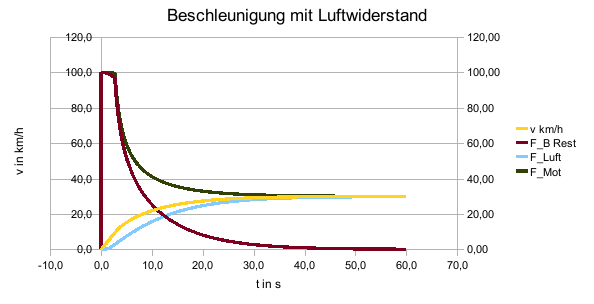
In der Tabelle oder dem Diagramm ist die Stagnation auf einen Grenzwert von ca. 30 km/h gut zu erkennen. Hier wurde vereinfacht vorherige Tabellenmethode zur Berechnung übernommen, indem der Windwiderstand anstelle anderer Widerstandswerte jeweils über den Geschwindigkeitswert des vorherigen Zeitschrittes berechnet wird. Für einfache Simulationen mit keinem Anspruch an hohe Genauigkeiten ist eine solche Vorgehensweise durchaus möglich.
Bei der Berechnung weitere Widerstände wären folgende Erweiterungen möglich:
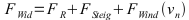
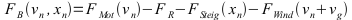
vg: Gegenwind
Tabelle für die Beschleunigungsfahrt mit allen Fahrwiderständen:
|
t |
X |
v |
v km/h |
a |
F_Ges |
F_Wind |
Wind m/s |
F_Steig |
Steigung in % |
F_Roll |
F_Mot |
P in W |
Pmax |
Fmax |
Gas |
|
-0,1 |
0,00 |
0,00 |
0,00 |
0,0 |
0,0 |
1,7 |
2,0 |
15,0 |
1,5 |
10,0 |
0,0 |
0,0 |
250 |
100 |
0 |
|
0,0 |
0,00 |
0,00 |
0,00 |
0,7 |
70,0 |
1,7 |
2,0 |
15,0 |
1,5 |
10,0 |
100,0 |
0,0 |
250 |
100 |
1 |
|
0,1 |
0,00 |
0,07 |
0,25 |
0,7 |
73,2 |
1,8 |
2,0 |
15,0 |
1,5 |
10,0 |
100,0 |
7,0 |
250 |
100 |
1 |
|
0,2 |
0,01 |
0,14 |
0,52 |
0,7 |
73,0 |
2,0 |
2,0 |
15,0 |
1,5 |
10,0 |
100,0 |
14,3 |
250 |
100 |
1 |
|
0,3 |
0,03 |
0,22 |
0,78 |
0,7 |
72,9 |
2,1 |
2,0 |
15,0 |
1,5 |
10,0 |
100,0 |
21,6 |
250 |
100 |
1 |
|
0,4 |
0,06 |
0,29 |
1,04 |
0,7 |
72,8 |
2,2 |
2,0 |
15,0 |
1,5 |
10,0 |
100,0 |
28,9 |
250 |
100 |
1 |
|
0,5 |
0,09 |
0,36 |
1,30 |
0,7 |
72,6 |
2,4 |
2,0 |
15,0 |
1,5 |
10,0 |
100,0 |
36,2 |
250 |
100 |
1 |
|
1,0 |
0,36 |
0,72 |
2,60 |
0,7 |
71,8 |
3,2 |
2,0 |
15,0 |
1,5 |
10,0 |
100,0 |
72,3 |
250 |
100 |
1 |
|
2,0 |
1,44 |
1,43 |
5,16 |
0,7 |
69,9 |
5,1 |
2,0 |
15,0 |
1,5 |
10,0 |
100,0 |
143,3 |
250 |
100 |
1 |
|
3,0 |
3,22 |
2,12 |
7,64 |
0,7 |
67,7 |
7,3 |
2,0 |
15,0 |
1,5 |
10,0 |
100,0 |
212,3 |
250 |
100 |
1 |
|
4,0 |
5,68 |
2,78 |
10,00 |
0,6 |
57,2 |
9,8 |
2,0 |
15,0 |
1,5 |
10,0 |
91,9 |
255,5 |
250 |
100 |
1 |
|
5,0 |
8,72 |
3,27 |
11,76 |
0,4 |
40,6 |
11,9 |
2,0 |
15,0 |
1,5 |
10,0 |
77,5 |
253,2 |
250 |
100 |
1 |
|
7,0 |
15,94 |
3,90 |
14,06 |
0,2 |
24,5 |
15,0 |
2,0 |
15,0 |
1,5 |
10,0 |
64,4 |
251,6 |
250 |
100 |
1 |
|
10,0 |
28,57 |
4,46 |
16,04 |
0,1 |
13,4 |
17,9 |
2,0 |
15,0 |
1,5 |
10,0 |
56,3 |
250,8 |
250 |
100 |
1 |
|
15,0 |
52,13 |
4,90 |
17,65 |
0,1 |
5,6 |
20,4 |
2,0 |
15,0 |
1,5 |
10,0 |
51,0 |
250,3 |
250 |
100 |
1 |
|
20,0 |
77,19 |
5,10 |
18,35 |
0,0 |
2,5 |
21,6 |
2,0 |
15,0 |
1,5 |
10,0 |
49,1 |
250,1 |
250 |
100 |
1 |
|
25,0 |
102,92 |
5,18 |
18,66 |
0,0 |
1,1 |
22,1 |
2,0 |
15,0 |
1,5 |
10,0 |
48,3 |
250,1 |
250 |
100 |
1 |
|
30,0 |
128,42 |
5,22 |
18,80 |
0,0 |
0,5 |
22,4 |
2,0 |
15,0 |
1,5 |
10,0 |
47,9 |
250,0 |
250 |
100 |
1 |
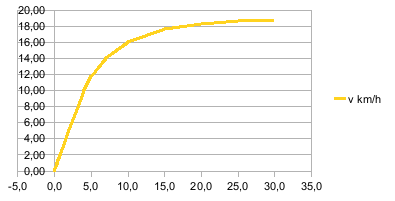
Verglichen mit anderen Diagramm ist hier gut zu sehen, dass die Endgeschwindigkeit wiederum auf einen Grenzwert zustrebt.
Das folgende Schaubild zeigt das Ablaufschema für eine erweiterte Simulation bei der auch ein Fahrweg mit unterschiedlichen Steigungen simuliert werden kann. Die Steigungen je Streckenstück werden über eine Verweisfunktion aus einer anderen Tabelle jeweils entnommen.
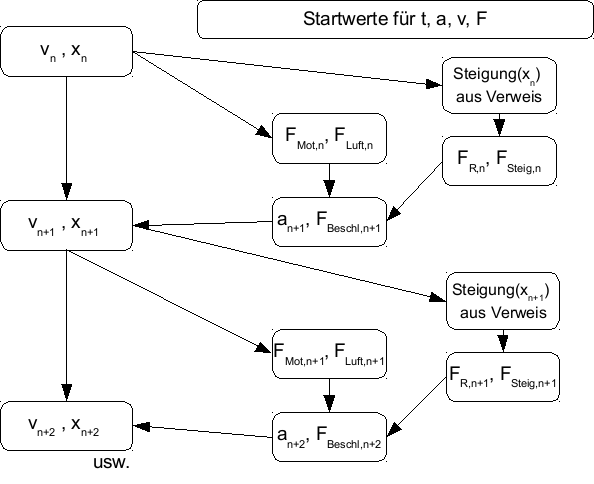
Eine einfache Methode stellt eine Höhenfahrt dar um die eigene Antriebsleistung zu ermitteln. Bei Windstille wird eine längere Steigung von mindestens 150m hoch gefahren und die Zeit gemessen, wie auch die Streckenlänge. Die Einschätzung, wie stark die eigene Anstrengung empfunden wurde, muss jeder ehrlich selbst treffen.
Eine Höhenfahrt von 150m in 30 min und dabei ca. 3,7..3,9 km Strecke gefahren ergäbe folgende Werte:
28Wh/100m*150m/0,5h=84W Hubleistung,
6N*3,9km/h /0,5h=13W Fahrwiderstand;
Insgesamt: 97W und durchschnittlich 3,85% Steigung
Wird bei einem Grundumsatz mit leichter Tätigkeit von einem Kalorienbedarf von 2000-2500 kKal ausgegangen, so entspricht das ungefähr 100kKal pro Stunde, am Tag etwas mehr und bei Nachtruhe etwas weniger. Bei einem Wirkungsgrad des Menschen von ca. 22% müßte dieser für 100W bzw. 100Wh mechanische Pedaltretleistung ungefähr 350 bis 400 kKal verbrauchen. Das wäre ungefähr das dreifache des stündlichen Tagesumsatzes an Kalorien.
Für Energie ist die SI-Einheit J und als weitere Einheit können Ws oder Wh verwendet werden. Da jedoch der Wirkungsgrad des Menschen bei der Umsetzung von der Energie in der Nahrung in mechanischer Arbeitsverrichtung eine ungenaue Größe darstellt, wird um beide Seiten besser auseinander halten zu können, hier gerne weiterhin kKal verwendet und kJ in Klammern ergänzt.
Am einfachsten funktioniert eine solche Messung mit Hilfe einer GPS-Logging Anwendung auf einem Smartphone. Bei Windstille wird mit dem Rad auf einer ebenen Strecke mit hoher Geschwindigkeit gefahren und ab einer bestimmten Stelle ausgerollt. Gleiches sollte in der Gegenrichtung auf der Strecke auch durchgeführt werden. Die Messungen sollten ein paar mal wiederholt werden.
Die Meßwerte können in gängigen Tabellenbearbeitungsprogrammen (EXCEL, OpenOffice Calc, Gnumeric) ausgewertet werden. Die Programme bieten eine Funktion durch die Punkte Ausgleichspolynome der zweiten Ordnung zu legen. Aus den ermittelten Koeffizienten können die Widerstandswerte abgeleitet werden.
Eine mehrfache Durchführung der Messung erlaubt es die Werte zur Erlangung einer besseren Genauigkeit zu mitteln. Ein Teil der Schwankungen der GPS-Werte kann hierdurch ausgeglichen werden. Die Rollversuche in der Gegenrichtung dienen dazu die Einflüsse von kleinen Gefällen und Gegenwinden zu korrigieren, da eine ideale ebene Strecke mit absolute Windstille nicht leicht zu finden ist.
Selbst aufgezeichnete GPS Daten unterliegen natürlich den Meßungenauigkeiten des Systems. Diese können bei den Simulationsberechnungen nicht vernachlässigt werden. Im Wesentlichen unterliegen die Daten,
starken Schwankungen bei den Höhenangaben und,
Zusätzlichen Schwankungen bei den Koordinaten.
Mit einfachen Rechenformeln können diese Fehler nicht ausgeglichen werden. Es ist nicht möglich ohne weiteres Wissen die Ergebnisse zu verbessern. Besonders störend sind die Schwankungen der Höhe bei,
einer kurzen Strecke, im ungünstigsten Fall Null Meter,
Größere Schwankungen zu Beginn der Aufzeichnung ,
Größere Schwankungen bei Absinken der Genauigkeit,
Wenn während der Messung neue Korrekturwerte aus der GPS-Datenübertragung verwendet werden.
Eine Abmilderung der durch die Ungenauigkeiten verursachen Auswirkungen kann über folgende Lösungsansätze erreicht werden:
Bei Streckenbeginn werden die Höhenwerte mit einer unterschiedlichen Bewertung in eine Glättungsberechnung einbezogen.
Die theoretisch gefahrenen Höhenwerte werden mitberechnet und aus dem Vergleich mit den Meßdaten wird ein sanfterer Verlauf erzielt.
Die Höhenwerte werden mittels Splines geglättet. Dabei müssen geeignete Abschnitte gewählt werden.
Die Weglänge geht bei einer Glättung in die Berechnung als Gewichtung mit ein. Unplausible Höhenunterschiede (Höhenschwankung 5m, 3m gefahren) werden dabei begrenzt.
Somit sollten die größten Ausreißer nicht mehr ein zu großes Problem darstellen. Eine Möglichkeit zur Verbesserung wäre eine mehrfache Meßfahrt der Strecke und die Mittelung der Werte. Eigene Messversuche ergaben bei zwei Fahrten der gleichen Strecke einen Höhenoffsetfehler von 15m bis 20m auf einer Strecke mit 40m Höhendifferenz. Für genauere Werte müßte die Strecke also mindestens drei bis vier mal gefahren werden. Der Algorithmus zur Glättung ist etwas aufwendig, da hier naheliegender Punkte geeignet zusammengefaßt werden müssen. Eine solche Funktion erfodert ein Programm in VBA und kann nicht mehr so ohne weiteres über Tabellenfunktionen realisiert werden.
Aus den Lat/Lon-Werten wäre es möglich die gefahrene Streckenlänge zur Sortierung der Punkte zu verwenden. Für kurze Streckenabschnitte ist dies durchaus möglich. Bei längeren Strecken ergibt sich bereits eine Abweichung, so dass die Reihenfolge der Punkte nicht mehr ganz passt am Ende. Mit einer manuellen Nachbearbeitung der Daten anhand mehrere Spalten berechneter Abstandswerte wäre hier natürlich möglich.
Ein einfacher Ansatz für die Gewichtung von mehreren Meßwerten:
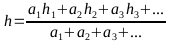
Wenn der erste Höhenwert mit einem niedrigen Gewicht in das Ergebnis eingehen soll:
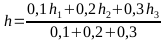
Wenn der Abstand des Streckenstückes gewichtet werden soll:
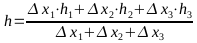
Wenn die Gewichtung der Streckenlänge und der Punkt am Streckenbeginn niedrig gewichtet wird:
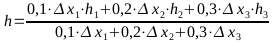
Die Höhe eines Punktes auf der Strecke könnte mit einer Gewichtung in Abhängigkeit von den Nachbarpunkten folgendermaßen geglättet werden:
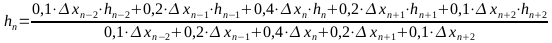
Bei der Berechnung der Höhen und auch der Steigung muss über eine Fallunterscheidung eine Division durch Null abgefangen werden. Zu hohe Steigungen auf Grund der Kenntnis der maximalen Steigung des Weges müssen begrenzt werden durch eine weitere Fallunterscheidung.Die Abweichungen bei den Höhen wird bei den Simulationsschritten notwendigerweise mitberechnet und sollte gedämpft bei den Steigungen einfließen. Zum Beispiel, dass eine Abweichung von 10m in eine zusätzliche Erhöhung der Steigung von 1% mündet.
Die Streckenabschnitte anhand der Werte für Latitude/Breitengrad und Longitude/Längengrad berechnen sich mittels Formeln für die Kugeloberflächen:
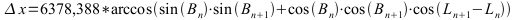
L: Längengrad; B: Breitengrad
Umrechnung von Grad in das Bogenmaß:
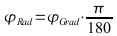
Für eine kleine Testfahrt sind hier die Punkte einmal nach der Reihenfolge und einmal nach der gefahrenen Strecke aufgetragen. Die schwankenden Höhenwerte sind gut zu erkennen. Die Genauigkeit zeigt, dass die Abweichungen der Höhenwerte nicht immer mit der Meßfehlerangabe korreliert.
Die gefahrene Strecke verläuft permanent einen Bach entlang bergauf. Vereinzelt gibt es fast flache Stellen und bei zwei kurzen Stücken gibt es ein Gefälle von ungefähr maximal 2 Meter. Für eine Simulation wären die Höhenwerte noch zu ungenau.
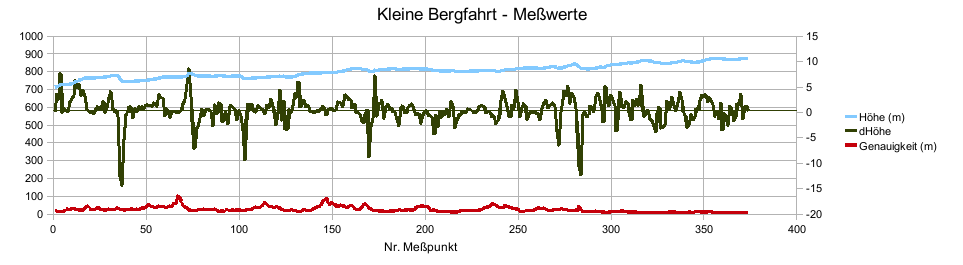
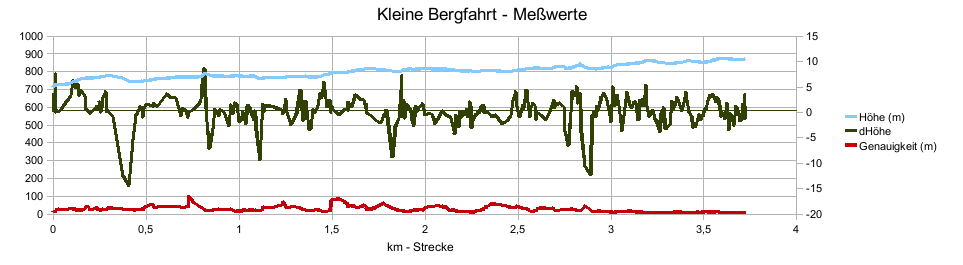
Anbei zum Vergleich die gleiche Strecke auf dem Rückweg gemessen:
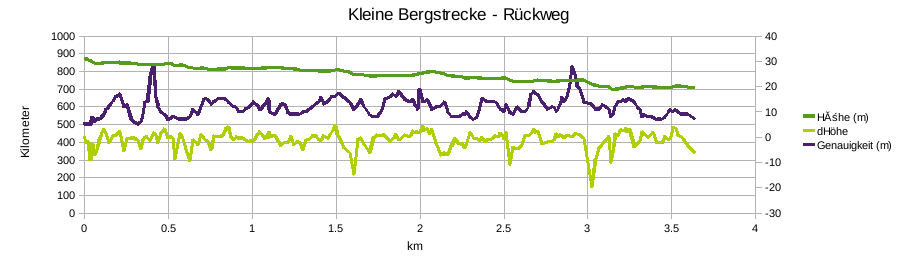
Anbei zu den ungenauen Meßwerten die Simulationsversuche mit einem Antrieb Fmax 100N und Pmax 250W:


Die Trägheit des Systems verursacht noch eine zusätzliche Glättung und somit wird der Verlauf in der Simulation viel runder bei den rückgerechneten Höhen.

Eine Simulation mit einer Tretleistung von Pmax 100W ergab fast auf die Minute genau die aufgewendete Fahrzeit bei der Messung der Strecke mit dem Fahrrad.
Da vor allem die Höhenwerte stark schwanken wäre es sinnvoll die Strecke mehrfach zu fahren und die Messwerte zu mitteln und von Ausreißern zu befreien. Bei längeren Strecken addieren sich aber die Meßfehler, so dass sich die Zahlen nicht mehr in Abhängigkeit von der gefahrenen Strecke einfach sortieren lassen. Bei einfachen und serpentinenfreien Strecken kann diese einfach über den Abstand der Punkte zu den Nachbarn realisiert werden. Der Zickzackverlauf der Kurve kann mit Hilfe von Mittelwertbildungen geglättet werden, falls in Gegenrichtung auf der anderen Straßenseite gefahren wurde. Die gemessene Strecke von 3,7 km auf einer Forststraße entlang eines kleinen Voralpenflusses ließ bereits eine solche einfache Zusammenführung nicht zu.
Eine gute Simulation des Gesamtsystems würde ein hinterlegtes Wirkungsgradkennlinienfeld berücksichtigen. In einer Tabellenkalkulationsanwendung wäre das eine sehr aufwendige Anwendung der Verweisfunktionen (Spalten und Zeilen gleichzeitig) erfordern. Die Nachbildung des Reglers würde mit gleicher Methode realisiert werden. Ein anderer Weg für die Simulation wäre das Kennlinienfeld über eine Polynomfunktion anzunähern und diese Formel zu verwenden. Solche aufwendigen Simulationen sollten besser mit entsprechenden Simulationsanwendungen durchgeführt werden. Einzelne Parameter lassen sich in Simulationsanwendungen viel einfacher variieren und die Ergebnisse grafisch darstellen.
In vielen Artikeln wurde der Effekt der Nutzbremsfahrten als gering eingestuft. Bei vielen Strecken in Deutschland, vor allem im Städten, wo die meisten Einwohner leben, dürften diese Werte zutreffen. Bei den Schätzungen wurden in der Regel auch die geringe Bremsleistungen von bis zu 100W des Systems berücksichtigt.
|
Pedelec-Fahrt mit Nutzbremse |
||||||
|
|
|
|
|
|
|
|
|
Eingebrachte Energie: |
|
|
|
|
|
|
|
100 |
Wh |
Radfahrer |
|
|
|
|
|
100 |
Wh |
Antrieb |
|
|
|
|
|
------------ |
|
|
|
|
|
|
|
200 |
Wh |
Gesamtenergie |
|
|
|
|
|
|
|
|
|
|
|
|
|
Aufteilung der Energie bergaufwärts: |
|
|
|
|
||
|
15 |
% |
Rollwiderstand |
|
|
|
|
|
10 |
% |
Luftwiderstand |
|
|
|
|
|
75 |
% |
Hubarbeit |
|
|
|
|
|
ergibt: |
|
|
|
|
|
|
|
30 |
Wh |
Rollwiderstand |
|
|
|
|
|
20 |
Wh |
Luftwiderstand |
|
|
|
|
|
150 |
Wh |
Hubarbeit |
|
|
|
|
|
|
|
|
|
|
|
|
|
150 |
Wh |
Hubenergie für Nutzbremse |
|
|
||
|
0 |
Wh |
Radfahrer (sofern noch mitstrampelt) |
|
|
||
|
------------ |
|
|
|
|
|
|
|
150 |
Wh |
Gesamtenergie |
|
|
|
|
|
|
|
|
|
|
|
|
|
Aufteilung der Energie bergabwärts: |
|
|
|
|
||
|
15 |
% |
Rollwiderstand |
|
|
|
|
|
20 |
% |
Luftwiderstand (bergab höher, da schneller) |
|
|||
|
65 |
% |
Hubarbeit (die verbremst werden müßte) |
|
|
||
|
ergibt: |
|
|
|
|
|
|
|
22,5 |
Wh |
Rollwiderstand |
|
|
|
|
|
30 |
Wh |
Luftwiderstand |
|
|
|
|
|
97,5 |
Wh |
Restenergie Hubarbeit für Nutzbremse |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wirkungsgradkette Radfahrer: |
|
|
|
|
||
|
0,90 |
|
Kette, Übersetzung; |
|
|
|
|
|
|
|
|
|
|
|
|
|
Wirkungsgradkette Antrieb: |
|
|
|
|
||
|
0,95 |
|
Akku interner Widerstand Entladung |
|
|
||
|
0,85 |
|
Schaltwandler Antriebsstrom (U und f) |
|
|
||
|
0,85 |
|
Motorwirkungsgrad (magn-mech) |
|
|
||
|
------------ |
|
|
|
|
|
|
|
0,69 |
|
Gesamtwirkungsgrad angetrieben |
|
|
||
|
|
|
|
|
|
|
|
|
Wirkungsgradkette Rekuperation: |
|
|
|
|
||
|
0,90 |
|
Akku mit internen Ladungsverlusten |
|
|
||
|
0,85 |
|
Schaltwandler Antriebsstrom (U und f) |
|
|
||
|
0,85 |
|
Motorwirkungsgrad (magn-mech) |
|
|
||
|
------------ |
|
|
|
|
|
|
|
0,65 |
|
Gesamtwirkungsgrad nutzgebremst |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
63,40 |
Wh |
Rekuperationsenergie mit Wirkungsgraden |
|
|
||
|
145,69 |
Wh |
Energieentnahme Akku mit Wirkungsgraden |
|
|
||
|
|
|
|
|
|
|
|
|
43,52 |
% |
Prozentuale Rückspeisung |
|
|
||
|
|
|
mit berücksichtigten Wirkungsgradverlusten |
|
|||
|
|
|
der Gesamtwirkungsgradketten |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Anmerkung: |
||||||
Die Bilanz für 100% Motorbetrieb bergauf und 100% Generatorbetrieb bergab wäre die Multiplikation aller Wirkungsgrade:
0,75 Hubarbeit mit Abzug der Verluste bergauf
0,69 Wirkungsgradkette Motorbetrieb
0,65 Hubarbeit mit Abzug der Verluste
0,65 Wirkungsgradkette Generatorbetrieb
Ergibt: 0,218 also rund 21%
Aus den beiden Beispielen lassen sich folgende Regeln erkennen:
Die ungünstigste Bilanz mit Rekuperation ergibt sich jeweils, wenn mit maximaler Motorunterstützung bergauf gefahren wurde.
Je mehr Energie über den Pedalantrieb aufgebracht wurde, desto besser wird die Bilanz mit Rekuperation.
Grob überschlagen für die meisten Bergstreckenprofile (Straßen, Forststraßen, Wege) würde sich folgendes Bild für die Verlängerung der Fahrtdauer in Abhängigkeit von der Bremsleistung ergeben:
|
max. Bremsleistung (Akkuladung in W): |
Prozentualer Gewinn: |
Prozent des maximal möglichen Wertes: |
|
0 W |
'0 % |
'0 % |
|
100 W |
15 %, |
'34 % |
|
200 W |
30 %, |
'68 % |
|
300 W |
38 %, |
'86 % |
|
400 W |
42 %, |
'95 % |
|
1 kW |
'44 % |
'99 % |
|
Unter der Voraussetzung die maximale Nutzbremsleistung wird bereits ab 15-20 km/h erreicht. Im weiteren wird dabei auch angenommen, dass mit Zunahme der Bremsleistung auch das maximale Moment im Generatorbetrieb des Motors zunimmt bis zur Leistung von 400W, danach nicht mehr. |
||
Ab einer Bremsleistung von 300W wird nur noch sehr wenig Rekuperationsenergie verschenkt, so dass sich ab hier ein weiterer Aufwand nicht mehr lohnt.
Bei mir würde der Gewinn unter Umständen etwas größer ausfallen, da ich bei den flacheren Gefällestücken zusätzlich wieder etwas in die Pedale treten würde, was wiederum der Energiegewinnung dienen würde. Der Grund wäre, dass die Bewegung die Abkühlung durch den Fahrtwind mildern würde. Nach der anstrengenden Hochfahrt, würden bergab die Beinmuskeln zu sehr kalt werden und verstärkt das Risiko für die eine oder andere negativen Folge (Muskelkater, Zerrungen, Krampf).
Zuletzt sei noch angemerkt, dass sich die niedrigen Werte einer Reichweitenverbesserung von nur 5% von Herstellern, die keine Rekuperation im Programm haben hiermit auch begründen läßt. Bei einer 90% Motorunterstützung könnten nach der Wirkungsgradkette ungefähr 24% erreicht werden, da aber nach dem Bremsprofil mit 100W Rekuperationsleistung nur durchschnittlich 34% genutzt werden können, ergibt sich ein Wert von 8% und wenn die Hälfte des Streckenprofils eben ist, dann ergeben sich nur 4% Reichweitenverlängerung.
Wird mit einer durchschnittlichen Motorunterstützung von 50% gerechnet, als Bremsprofil angenommen, dass man nicht viel steile Downhillstrecken bergab fährt, dann kann natürlich bei nur maximal 100W Rekuperationsleistung durchschnittlich ungefähr die Hälfte genutzt werden. Dort wo man gerne mit dem Pedelec fährt, ist nur ein drittel der Straßen eben. Es kann somit viel mehr zurückgespeist werden und liegt im Bereich von 15% Reichweitenverlängerung.
Ein Fahrer, der sich kennlinienoptimiert verhält, kann natürlich mit angepasster Fahrweise auch mit nur maximal 100W Rekuperationsleistung 30% Reichweitenverlängerung erreichen. Da dies aber auch nur ein Bruchteil der Ingenieure und Physiker beim Pedelecfahren so hinbekommen (das Problem es selbst in die Praxis umzusetzen), hat dies keine große Bedeutung auf dem Markt. Bei maximalen Rekuperationsleistungen im Bereich von 200W bis 300W ist es nicht mehr notwendig sich kennlinienoptimiert zu verhalten um deutlich bessere Reichweitenverlängerungen mittels Rekuperation zu erreichen.
Li-Akkus sind empfindlicher als NiMh und haben daher besondere Schutzschaltungen integriert. Die Zellen müssen vor Tiefentladung, Überladung und zu großer Erwärmung geschützt werden. Für die Ladung und auch die Entladung gibt es daher besondere Balancer-Schaltungen für jede Zelle. Diese Schutzkomponenten begrenzen die Leistungen am stärksten bei der Energieaufnahme. Somit liegen die maximalen Rückspeisungsleistungen meistens im Bereich von einem drittel bis einem viertel der Kapazität des Lithiumakkupacks. Aus dem Grunde haben die Pedelecs eine Rückspeisung von maximal 100W ab Akkukapazitäten von 300 bis 350 Wh. Somit konnte die Rekuperation erst ab der Verwendung von größere Akkukapazitäten zugelassen werden.
Mit NiMh (Standardzellen) würde ein Akkupack mit 60 Wh zwischen 600-700 Gramm wiegen. Diese können je nach Belastungsdauer entsprechend höhere Rückspeiseströme vertragen. Je nach Typ und Wärmezustand wären zwei bis fünf Minuten bis zum vierfachen als Peakleistung in W gegenüber der Kapazität in Wh (Ladung mit max. 4C) möglich. Die NiMh-Akkus sind also viel unkritischer und der Gewichtsnachteil ist überraschenderweise gar nicht so groß.
Auf Grund der flachen Spannungskennlie gegenüber dem Ladungszustand ist es bei diesem Typ schwieriger eine Anzeige der vorhandenen Kapazität für eine Reichweitenanzeige zu realisieren. Das ist ein selten erwähnter Hauptpunkt, warum sich die Hersteller bei E-Bike und auch E-Auto fast durchwegs Li-Akkus bevorzugen. Es wäre für die Rückspeisung aber durchaus interessant hier beide Typen geschickt zu kombinieren.
Der Vorteil der Rekuperation hängt stark von dem Profil der Fahrtstrecke ab und auch des Fahrverhaltens des Radlers. Die Fahrer mit komplett fehlenden Physikkenntnissen können natürlich nicht ihren Fahrstil so anpassen um den maximalen Vorteil aus dieser Technik zu ziehen.
Für meine vorgesehenen Fahrten wäre diese Technik sehr zu wünschen. Häufig würde ich mit dem Rad einen Forstweg entlang eines Baches am Beginn der Alpen hochfahren. Die Unterstützung herbei wäre meistens bergauf zwischen 25 bis 50%. Die gleiche Strecke würde ich Rückwärts rollen und statt dauernd an der Bremse zu hängen, würde ich hier die Rekuperation intensivst nutzen. Ich muss dabei real etwas über 50% der Energie bei der Abfahrt über die Bremse vernichten. Das hat schon einige Bremsklötze verschlissen und die Felgen sehen mittlerweile schlimm aus.
Damit die Rekuperation eine entsprechend akzeptable Abbremsung bei den meisten Bergabfahrten liefern kann, müßte der Energiespeicher eine Leistungsaufnahmefähigkeit von 200W aufweisen. Bei einer Leistung von nur 100W gibt es bei den Bergstrecken noch zu viele Abschnitte, für die diese Bremsleistung einfach noch zu gering ist und verhältnismäßig viel noch mechanisch gebremst werden muss.
Mit:
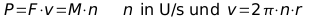
ergibt sich:
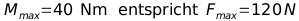
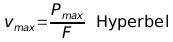
Für ein Gesamtgewicht von Rad plus Fahrer von 100kg und 100W maximale Bremsleistung ergeben sich folgende Höchstgeschwindigkeiten:
|
Gefälle in % |
Resultierende Kraft F in Gefällerichtung |
Maximale Geschwindigkeit für 100W Bremsleistung |
Bemerkungen |
|
'2 % |
20 N |
18 km/h (>25km/h für 200W) |
Bei höheren Geschwindigkeiten nur noch Teilbremsung. |
|
'4 % |
40 N |
9 km/h (18km/h für 200W) |
Bei höheren Geschwindigkeiten nur noch Teilbremsung und das Rad wird schneller bis der Luftwiderstand den weiteren Anstieg begrenzt. |
|
'10 % |
100 N |
4 km/h (8km/h für 200W) |
Bei der niedrigen Geschwindigkeit sinkt im Generatorbetrieb das maximale Moment. Somit nur noch Teilbremsung. Außnahme sinusoidal conrol with complementay PWM kann hier noch Vollbremsung. |
|
'12 % |
120 N (40 Nm) |
3 km/h (6km/h für 200W) |
Bei der niedrigen Geschwindigkeit sinkt im Generatorbetrieb das maximale Moment. Somit nur noch Teilbremsung. Außnahme sinusoidal conrol with complementay PWM kann hier noch Vollbremsung. |
|
>'12 % |
>120 N (>40 Nm) |
Nur noch Teilbremsung |
Nur noch Teilbremsung möglich. Unabhängig von der maximalen Leistung der Rekuperation. Für Vollbremsung Motoren mit höherem maximalen Moment d.h. auch im Bremsbetrieb notwendig. |
|
'20 % |
204 N |
Nur noch Teilbremsung |
Nur noch Teilbremsung möglich. Unabhängig von der maximalen Leistung der Rekuperation. Für Vollbremsung Motoren mit höherem maximalen Moment d.h. auch im Bremsbetrieb notwendig. Hier ca. 70 Nm. |
Anzumerken wäre noch, dass Steuerungen der Technik „Sinusoidal Motor Control mit Complementary Bipolar/Uniplar PWM (4 Quadranten)“ so gesteuert werden können, dass das maximale Bremsmoment bis zum vollständigen Stillstand möglich ist.
Anhand der Tabelle läßt sich gut ablesen, wo die technischen Grenzen liegen bei der Rekuperation und die eine oder andere Frage aus vorherigen Kapitel dürfte sich somit klären. Nicht nur die maximale Rekuperationsleistung müßte mindestens 200W betragen, sondern auch des maximale Moment des Antriebes (Umgerechnet auf des 26'-Hinterrad) müßte mindestens 80Nm betragen um ein gutes Rekuperationsverhältnis zu ermöglichen.
Damit können gut zwei Drittel der Energie im Streckenmix (bergiges und hügeliges Gelände) geerntet werden. Aus dem verbleibenden Drittel würde eine Erhöhung der maximalen Rekuperationsleistung am meisten plus beim Energieernteergebnis bringen. Mehr Moment bringt dann nur bei einem Fahrstiel mit vielen sehr steilen Gefällestrecken im Gelände. Somit ergibt sich folgendes Ranking für die Ausnutzung Rekuperation beim Pedelec:
M: 40Nn & Prekuperation: 100W
M: 60..80Nm & Prekuperation: 200W
M: 80Nm & Prekuperation: 300..400W
M: 120Nm & Prekuperation: 400..500W
Anzumerken wäre noch, das ab der dritten Stufe der Aufwand gebenüber dem zusätzlichen Recuperationsenergieertrag überproportional steigt. Der Unterschied für die Auslegung der Rekuperation zwischen dem 25km/h und 45km/h Pedelec ist dabei gering. Es wird beim 45km/h Modell empfohlen bei den Stufen jeweils bei der Auslegung an der maximalen Leistung auszulegen.
Bei Momenten über 80 Nm, die auch Steigungen oder Gefälle über 24% rekuperieren, wird es notwendig werden einen Teil des bremsenden Generatormomentes auf Vorderrad zu legen. Im Gelände auf gekiesten Forststraßen oder Wegen ähnlicher schwieriger Zustände würde das Hinterrad sonst zu sehr zum Rutschen oder Kurzblockieren neigen. Beim Vorderrad muss allerdings auch das Bremsmoment abrupt abgebrochen werden können mit mindestens den gleichen kurzen Reaktionszeiten, wie die mechanische Hebelbremse am Lenkrad damit die Zahl der Stürze nicht auf Grund der Technik steigt. Sehr steile Gefälle sollten sowieso langsam gefahren werden. Die Geschwindigkeit sollte dabei im Bereich des zu Fuß Gehens liegen. Gleichzeitig hilft das auch die Auslegung der maximale Rekuperationsleistung im Zaum zu halten.
Eine interessante Entwicklung stellt der Radfelgenmotor von der Firma Velogical (Köln) dar. Für die Nachrüstung bei normalen Fahrrädern als Dauerlösung oder auch nur bei Bedarf stellt dies eine interessante Lösung dar.
In der Vergangenheit gab es auch verschiedene Lösungen mit angedrückten Rollen auf dem Radmantel. Die Lösung mit zwei gegenüberliegenden Felgenmotoren ist meiner Ansicht nach hier eine wesentlich technisch bessere und gelungene Alternative.
Von den Ausführungen mit Rollen auf den Radmantel meiner Ansicht nach die gelungenste Lösung gibt es von der Firma add-e in Österreich bei Villach, die einen Reibradantrieb anbietet, der am Rahmen zwischen Tretlager und Rad montiert wird. An dieser Position befanden sich bei vielen Fahrrädern früher der Ständer. Das Reibrad hat ungefähr einen Durchmesser von 6cm und liegt auf der Lauffläche auf. Für die Nachrüstung bei normalen Fahrrädern als Dauerlösung oder auch nur bei Bedarf stellt dies eine interessante Lösung dar.
Bei Antriebe (Velospeeder und add-e) nutzen das Moment, dass sich bei schräger Ausrichtung ergibt um dadurch eine Antriebskraftabhängigkeit des Andruckes nutzen zu konnen. Ein mehr an Moment führt zu erwünschtem höherem Anpressdruck. Bei geringerem Moment ist der Anpressdruck geringer und die mechanischen Verluste werden dadurch auch reduziert.
Im Bremsbetrieb sind die Kraftrichtung leider umgekehrt. Dadurch fällt bei der Rückspeisung das maximale Moment im Generatorbetrieb geringer aus als im Motorbetrieb. Im niedrigen Geschwindigkeitsbereich bleiben damit diese beiden Lösungen bei der Bremswirkung hinter den Hinterradmotoren noch zurück. Auf der anderen Seite können diese Antriebsmotoren viel günstiger als Hinterradmotoren hergestellt werden, so dass durchaus ein weiterer Motor in umgekehrter schräger Ausrichtung jeweils für den Bremsbetrieb und als Leistungsgenerator für Beleuchtung oder Laden beim Fahren oder aufgebockt als Fitnessgerät verwendet werden könnte. Eine zusätzliche hinzuschaltbare Feder zur Erhöhung des Andruckes wäre auch eine denkbare Lösung ohne weitere Motoren zu benötigen.
Beim bürstenlosen Motor BLDC ist der Unterschied für die 1 bis 4 Quadrantenfähigkeit einzig in der Ansteuerung begründet.
Six Step Motor Control (Methode für Phasenumlauf/Drehung)
Sinusoidal Motor Control (Methode für Phasenumlauf/Drehung)
Independent Bipolar/Unipolar PWM (2 Quadranten)
Complementary Bipola/Uniplar PWM (4 Quadranten)
Diese gibt es als kleinen SMD-Vielfüssler, die jeweils 6 MOSFET ansteuern. Für 4Q wird das Gehäuse mit vier Pins mehr gewählt um die zwei weiteren benötigten Anschlüsse zur Verfügung zu stellen. Die Mosfets sind in der Regel identisch und auch die maximalen Leistungsdaten unterscheiden sich nur geringfügig (ca. 10%). Wenn ein 1Q SMD-IC vielleicht zwei Euro kostet, kostet ein 4Q SMD-IC halt noch 5 Euro.
Ergänzung des Vergleichs um die Antriebsart des Radfelgenmotors Velospeeder und Reibradantriebes von add-e :
|
Vergleich der Antriebsarten |
|
|
|||
|
Eigenschaften |
Mittenmotor |
Vorderradmotor |
Hinterradmotor |
Velospeeder Radfelgenmotor |
Add-e Reibradantrieb |
|
Rahmen: |
Benötigt eigens konstruierten Rahmen im Bereich der Tretlager. |
Keine Änderung und kann in die meisten Rahmen eingebaut werden. |
Keine Änderung und kann in die meisten Rahmen eingebaut werden. |
Keine Änderung und kann in die meisten Rahmen eingebaut werden. |
Keine Änderung und kann in die meisten Rahmen eingebaut werden. Ggf. Hinterradständer anbauen. |
|
Bausätze: |
Es gibt Bausätze, bei denen muß der Rahmen bearbeitet werden. |
Ja, gbt es. |
Ja, gibt es. |
Ja, kann zum Selbsteinbau bezogen werden. |
Ja, kann zum Selbsteinbau bezogen werden. |
|
Motorgewicht: |
3-4 kg |
3kg (Getriebemotor) 3,5-5kg (Getriebeloser Motor) |
3kg (Getriebemotor) 3,5-5kg (Getriebeloser Motor) |
ca. 1,6 kg (alle zwei Motoren zusammen mit Halterungen) |
ca. 2-3 kg (Motoren zusammen mit Halterungen) |
|
max. Drehmomente: |
27-60 Nm |
27-60 Nm |
27-60 Nm |
40 Nm (gemäß Email bereits auch mehr erreicht) |
ca. 80 Nm errrechnet (gemäß Email, Übersetzung gerechnet) |
|
Schwerpunktlage: |
Liegt tiefer als bei Radnabenmotoren |
Liegt höher als bei Mittenmotoren. |
Liegt höher als bei Mittenmotoren. |
Einfluss vernachlässigbar, da geringstes Motorgewicht. |
Geringer und tiefer als bei Mittenmotoren.
|
|
Ruperation / Nutzbremsbetrieb |
Nicht möglich, wegen Freilauf. (Freilauf der Kettenschaltung) |
Nicht möglich bei Motoren mit Freilauf. Ja, ist möglich, aber auf dem Markt kaum erhältlich. |
Nicht möglich bei Motoren mit Freilauf. Ja, gibt es auf dem Markt. (meist auf max. 100W begrenzt) |
Technisch möglich, bei dem Modell 2014 und auch 2015 noch nicht realisiert. |
Technisch möglich, nicht realisiert. |
|
Verschleiß Kette |
Erhöht den Verschleiß der Kette, da der Antrieb auf die Kette wirkt. |
Kein Mehrverschleiß der Kette.
|
Kein Mehrverschleiß der Kette. |
Kein Mehrverschleiß der Kette. |
Kein Mehrverschleiß der Kette. |
|
Verschleiß Zahnkränze |
Erhöht den Verschleiß der Zahnkränze, da der Antrieb auf die Kette wirkt. |
Kein Mehrverschleiß der Zahnkränze. |
Kein Mehrverschleiß der Zahnkränze. |
Kein Mehrverschleiß der Zahnkränze. |
Kein Mehrverschleiß der Zahnkränze. |
|
Mitnutzung von Übersetzungen |
Ja, da der Antrieb auf die Kette wirkt bzw. auf die Tretachse. |
Nein, da der Antrieb direkt auf das Rad wirkt.
|
In der Regel Nein, da der Antrieb direkt auf das Rad wirkt. Es gibt aber Varianten mit integrierten Nabengetriebe, die die Übersetzung mit nutzen. |
Nein, da der Antrieb direkt auf das Rad wirkt. |
Nein, da der Antrieb direkt auf das Rad wirkt. |
|
Verschleiß Felgen |
Nein |
Nein |
Nein |
Gering (Gummiring auf Alu oder Stahl, Verschleiß durch Felgenbremse ist höher; mit Nutzbremse geringerer Verschleiß, als andere Modelle ohne Nutzbremse). |
Nein. Der Verschleiß des Mantels ist etwas höher, dh etwas früher das Profil abgelaufen. Meist altern jedoch die Mäntel schneller, so dass dies kostenneutral bleibt. |
|
Verschleiß-/Ausfallgefährdung Antriebsmotormodule |
hoch: Getriebe des Tretlagerantriebes: |
a) mittel: Planetengetriebe (meist wechselbar) b) entfällt bei getriebelosen Direktantriebsmotor |
a) mittel: Planetengetriebe (meist wechselbar) b) entfällt bei getriebelosen Direktantriebsmotor |
mittel bis hoch: Gummiring, aber leicht zu wechselndes Verschleißteil
|
Mittel: Reibrad Haftbelag leicht zu wechselndes Teil. |
|
Fail safe Optionen in Verbindung mit Verschleiß |
Kette, Zahnkränze, bei Ausfall, nur noch Schieben möglich. |
Anfahrhilfe bis 6km sofern vorhanden kann noch verwendet werden. |
Anfahrhilfe bis 6km sofern vorhanden kann noch verwendet werden. Wenn Übersetzungen mit genutzt werden, nur Schieben möglich. |
Anfahrhilfe bis 6km sofern vorhanden kann noch verwendet werden. |
Anfahrhilfe bis 6km sofern vorhanden kann noch verwendet werden. |
|
Fail safe Optionen in Verbindung mit Motorausfall oder Steuerungsausfall. |
Bei einigen Modellen kann auch der Tretantrieb nicht mehr nutzbar sein. |
Fortsetzung der Fahrt mit Tretantrieb ohne Motorunterstützung. |
Fortsetzung der Fahrt mit Tretantrieb ohne Motorunterstützung. Wenn Übersetzungen mit genutzt werden, nur Schieben möglich. |
Fortsetzung der Fahrt mit Tretantrieb ohne Motorunterstützung. Motor kann auch abgebaut werden. |
Fortsetzung der Fahrt mit Tretantrieb ohne Motorunterstützung. Motor kann auch abgebaut werden. |
|
Mitnahme Antriebskomponenten in ein anderes Rad. |
In der Regel nicht möglich. |
Meistens möglich Komponenten in ein anderes normales Rad einzubauen für versierte Bastler. |
Meistens möglich Komponenten in ein anderes normales Rad einzubauen für versierte Bastler. |
Problemloser Umbau in ein anderes Rad möglich. |
Problemloser Umbau in ein anderes Rad möglich. |
|
Weiternutzung als nur normales Rad ohne Antrieb. |
Bedingt möglich. |
Normale Hinterradfelge ohne Motor einbauen und E-Teile abmontieren. |
Normale Hinterradfelge ohne Motor einbauen und E-Teile abmontieren. |
Der Motor kann weggeklappt werden. Somit wie normales Rad zu fahren. Motor kann auch abgebaut werden. |
Der Motor kann weggeklappt werden. Somit wie normales Rad zu fahren. Motor kann auch abgebaut werden. |
|
Umbau (Radrahmen) auf anderes Produkt anderer Hersteller. |
Rahmen in der Regel so spezifisch, dass nur Produkte des Herstellers verwendet werden können, solange diese noch erhältlich sind. |
In der Regel Produkte anderer Hersteller einbaubar. |
In der Regel Produkte anderer Hersteller einbaubar. |
In der Regel Produkte anderer oder des gleichen Herstellers einbaubar, sogar auch als zusätzliches System; |
In der Regel Produkte anderer oder des gleichen Herstellers einbaubar, sogar auch als zusätzliches System; |
|
Ggf. eingebaute Sensoren: |
Temperatursensor, Hallsensor |
Temperatursensor, Hallsensor |
Temperatursensor, Hallsensor |
Temperatursensor, Hallsensor |
Temperatursensor, Hallsensor |
|
Spannungsbereiche: |
erhältlich für 24-48V |
erhältlich für 24-48V |
erhältlich für 24-48V |
24-48V, je nach Antriebsleistung (für 25/45km/h) |
24-48V, je nach Antriebsleistung (für 25/45km/h) |
|
Verschiebung Optimumspunkt: |
Verschiebung, da Übersetzungen mit genutzt werden. |
Nicht verschiebbar. |
a) Nicht verschiebbar. b) Verschiebbar bei Motoren mit speziellen Zusatzwicklungen oder Steuerung der Polpaarzahl. c)Verschiebung, wenn Übersetzungen (z.B. spez. integr. Nabenschaltung) mit genutzt werden. |
a) Nicht verschiebbar. b) Verschiebbar bei Motoren mit speziellen Zusatzwicklungen oder Steuerung der Polpaarzahl. |
a) Nicht verschiebbar. b) Verschiebbar bei Motoren mit speziellen Zusatzwicklungen oder Steuerung der Polpaarzahl. |
|
Besonderer Schutz vor Entwendung |
Nur Abbau Steuerung und Akku möglich. |
Nur Abbau Steuerung und Akku möglich. |
Nur Abbau Steuerung und Akku möglich. |
Abbau Steuerung und Akku möglich. Motor ebenfalls abbaubar. |
Abbau Steuerung und Akku möglich. Motor ebenfalls abbaubar. |
Bei Gelegenheit wird der Text fortgesetzt oder auch nicht.
Literaturquellen:
Quellen zur rechtlichen Einstufung der Fahrräder mit Hilfsantrieben:
http://www.pedelecforum.de/forum/index.php?threads/e-bikes-und-pedelecs-die-aktuelle-rechtslage-auf-einem-blick.20746/
http://www.jmw-online.com/elektrofahrrad-pedelec-ebike.html
http://www.pedelecforum.de/wiki/doku.php?id=rechtliches:start
Ausführungen mit Rückspeisung habe oft keinen Freilauf:
http://pedelec-elektro-fahrrad.de/technik/rekuperation-bei-pedelecs/
Formeln und physikalische Werte:
Formeln der Physik und Tabellen der Physik. Taschenbuch der Physik, Horst Kuchling (Autor), Auflage von 1988, Verlag Harri Deutsch Thun Frankfurt am Main;
Zu den Akkus:
http://www.aufs-rad.de/elektroraeder/wissenswertes-zum-antrieb-der-akkumulator.html
Fahrwiderstände:
http://de.wikipedia.org/wiki/Fahrwiderstand
http://lustaufzukunft.de/pivit/aero/formel.html
http://www.leifiphysik.de/themenbereiche/einfache-maschinen/lb/physik-beim-radfahren-iv- fahrwiderstaende-beim-radfahren-0
http://www.physik.uni-wuerzburg.de/fileadmin/11010700/Didaktik/Zulassungsarbeiten/HA_1622196_Bielmeier_Carsten.p df
http://www.kreuzotter.de/deutsch/speed.htm
http://www.3dfraesstudio.de/LUFTW.HTM
Kalorienverbrauch des Menschen:
http://www.ernaehrung.de/tipps/allgemeine_infos/ernaehr10.php
http://www.supermass.com/Wieviele-Kalorien-verbraucht-ein-Mensch-taeglich/cp/70/de
Abstand GPS-Punkte:
http://www.kompf.de/gps/distcalc.html
Vergleich von Pedelecs:
http://extraenergy.org/main.php
Technik der Antriebe, Motoren und Zubehör:
http://elfkw.at/technik/motoren
Script mit Grundlagen, Versuchen und Aufgaben ( PDF) - Carl-Engler, Otto Bubbers, ces.karlsruhe.de, Elektromobilitaet_TGJ14:
http://ces.karlsruhe.de/~BUB/Umwelttechnik/Elektromobilitaet_TGJ14_2012.pdf
Artikel aus 2012 (nicht alles wird so mitgetragen):
http://e-bike-test.org/ebike-kaufberatung/energieruckgewinnung-rekuperation-ebikes/
http://www.adfc-bo.de/pedelec2012.htm
Interessante Entwicklung und Produkt für die Nachrüstung:
http://www.velogical-engineering.com/home-en
http://www.velogical-engineering.com/
http://www.ebike-news.de/velospeeder-leichtester-e-bike-nachruestsatz-fuer-fahrraeder-mit-16-kg-und-600-watt/7348/
http://www.ingenieur.de/Themen/Fahrrad/Der-leichte-Velospeeder-bringt-elektrischen-Rueckenwind-ans-Fahrrad
Und noch einen anderen Antrieb fürs Pedelec habe ich gefunden.
Nach dem beidseitigen Felgenmotor Velospeeder von Velogical in Köln, gibt es von einer Firma in Österreich bei/in Villach noch einen Reibradantrieb.
http://www.add-e.at/